連続標本空間で起こるランダムな事象は、問題の性質によるものと解の性質によるものの少なくとも 2 つの理由で、幾何学的なイメージを呼び起こすことがあります。 後者は、幾何学的図形の面積を比較することで、何度でも再解決が可能である。 一般に、幾何学的確率とは、ある領域に対して、ある規則に従って負でない量（1を超えない量）を割り当てることであると考えることができる。 この割り当てを領域Dに定義したものを関数μとすると、例えば、

0 ≦ μ(A) ≦ 1, A⊂ D and
μ(D) = 1

関数μは通常すべてのA⊂Dに対して定義されているわけではなく、μが定義されているDの部分集合は特定のサンプル空間を形成するランダムイベントとなる。 非常に多くの場合、μは面積の比によって定義されるので、σ(A)を集合Aの「面積」と定義すると、μ(A) = σ(A)/σ(D) とすることができる。

問題1

同じ駅から地下鉄で仕事に行く友人2人は、朝の7時から7時20分の間にランダムに駅に到着する。 彼らは互いに5分間待つことを望んでおり、その後、一緒でも一人でも電車に乗る。 2人が駅で出会う確率は何％か。

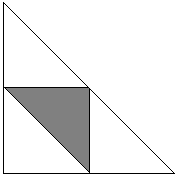
直交座標系（s, t）において、辺20（分）の正方形は、2人の友人が朝に地下鉄駅に到着する可能性をすべて表している。

灰色の領域Aはt = s + 5とt = s – 5という二つの直線で囲まれ、A内部では｜s – t｜ ≦ 5となる。 この確率はAの面積と正方形の面積の比で与えられる：

/ 400 = 175/400 = 7/16.

問題2

(.)

3点A、B、Cが半径1の円上にランダムに置かれている。 ΔABCが鋭角になる確率は？

点Cを固定し、点A、Bの位置はCから2方向に伸びる円弧α、βで定義される。 先験的に0 < α + β < 2πであることが分かっている。 この問題で好ましいαとβの値（鋭角の引き合いとして）は、0 < α < πと0 < πで、その和がπより小さいと角Cが鈍角になるので、α + β > πとなります。 下図は正方形の辺が2πの場合です。

領域Dは0 < α、0 < β、α＋β < 2πの3つの半平面の交点です。 これが上図の大三角形である。 有利な事象は、α＜1679＞π、β＜1679＞π、α＋β＜9137＞πの半平面が交わる斜線の三角形に属する。 この二つの面積比は明らかに1/4である。

ここで、ランダム三角形が鋭角でなければ、3点A,B,Cのうち2点が直径になる確率は0なので、鈍角と考えることができます（BCが直径となるには、α+β=πとなり、これは直線となるので面積の割り当てとしては0のみが可能であることになります）。 したがって、ΔABCが鈍角である確率は3/4と言える。 鈍角三角形の場合、円は2つに分割され、三角形は半分のうちの1つにすっぽり収まる。

半径1の円上に3点A、B、Cを無作為に置く。 3つとも半円になる確率は？

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometric Probabilities
• ほとんどの三角形は鈍角か？
  • 六つのセクターで八つの選択
  • 円上の三つのランダムな点
• 幾何学的確率
  • 三つに割った棒（トリリニア座標）
  • 三つに割った棒（トリトリリニア座標）. 直交座標での解法
• バートランドのパラドックス
• Birds On a Wire（問題と対話式シミュレーション）
  • Birds on a Wire: 解決策 by Nathan Bowler
  • Birds on a Wire（電線の上の鳥）。 Mark Huber氏による解答
  • Birds on a Wire: 確率論的シミュレーション。 Moshe Eliner氏による解答
  • Birds on a Wire（電線の上の鳥）。 Stuart Anderson氏による解答
  • Birds on a Wire（電線の上の鳥）。 Bogdan Lataianu氏による解答
• Buffonの麺シミュレーション
• Averaging Raindrops – an exercise in geometric probability
  • Averaging Raindrops, Part 2
• Rectangle on a Chessboard: 序章
• 棒に印をつけたり折ったりする
• 線分上のランダム点
• 半円の範囲
• 半球の範囲
• 重なったランダム間隔
• ランダムな区間 with One Dominant
• 正方形グリッド上の点
• 球面上の平面確率
• 三角形の確率

|コンタクト|フロントページ|コンテンツ|上|

Copyright © 1996->Contents: Catch-up!2018 アレクサンダー・ボゴモルニー