流体中の低レイノルズ数の泳者との類似性に触発されて、我々は力と運動を予測するために粒状媒体の最初の抵抗力理論を作成しました。 そのキーとなる考え方は重ね合わせの原理で、粒状媒体中を任意の軌道で移動する複雑な形状の体や足にかかる力は、それぞれの要素にかかる力の重ね合わせでうまく近似できる（図1）。 低レイノルズ数の泳者では、慣性効果が無視できるため、要素周囲の流体流れは十分に局所的であり、要素に作用する粒状力は他の要素に作用する力とは独立であるため、この積分原理は有効である。 このことを考えると、抵抗力理論も粒状媒体に有効であるという仮説を立てた。

図1. 抵抗力理論の重ね合わせ原理

抵抗力測定

動物やロボットは複雑な形態と運動をしているので、体や足の各要素は深さが異なるだけでなく、向きや移動方向も異なることがある（図1左）。 レイノルズ数の小さい流体中の遊泳では、力が向きや方向にどのように依存するかは、ストークスの法則から導き出すことができる。 しかし、粒状媒体の場合、そのような方程式が存在しないため、力がどのように依存するのかがわかりません。 そこで、私たちは板状の要素を用いて、侵入者の向きと方向の関数として粒状力を初めて測定しました（図1、右）。

その結果、力（応力）が向きと方向の両方に敏感に依存することがわかりました（図2、左）。 図2左）。プレートの侵入者が水平に向き、下向きに貫入しているとき、垂直方向の力は最大となる。 しかし、方向が水平からずれたり、下向きになったりすると、垂直方向の力は急速に減少する。 抵抗力の測定と理論の検証。

抵抗力理論の検証

粒状抵抗力の測定結果を用いて、脚の要素にかかる応力を積分し、抵抗力理論が粒状媒体中を移動するロボット脚の総揚力と抗力をよく予測できることがわかった（図2、右）。 重ね合わせの原理により、このモデルは任意の形状と軌道の脚に対して正確である。

Predictive Power of Resistive Force Theory

我々は、粒状媒体中で回転するロボット脚（規定運動学）の抵抗力理論を検証した後、粒状媒体上を自由に動くロボットに対してその予測力をテストしてみた。 我々は、歩幅と脚の曲率を広範囲に変化させたカスタム脚ロボットを粒状媒体上で動作させた。 先に述べたように、ロボットは凸面の脚を前に向けるよりも後ろに向ける方が速く動く。

次に、ロボットのマルチボディ動的シミュレーションを開発し、抵抗力理論を用いて、要素力の統合によりロボットのボディと脚にかかる揚力と抗力を計算した。 抵抗力理論を用いたシミュレーションで予測される運動ダイナミクスは、実験観察とよく一致することがわかった。

実験とシミュレーションを比較した結果、抵抗力理論は歩幅と脚曲率の広い範囲にわたって粒状媒体上の脚の運動性を正確かつ迅速に予測できることがわかった（Fig.3）。 抵抗力理論が粒状媒体上の脚式ロボットの動きを予測する。

我々の抵抗力理論により、流体の空気力学や流体力学に類似した粒状媒体中の力と動きを定量的に予測できるため、流動性地面の最初のテラダイナミクスを確立することができた。

抵抗力理論の汎用性

粒径、形状、摩擦、密度、圧縮度、多分散度などが異なる多様な粒状媒体の抵抗力測定を行った。 その結果、力の侵入方向と方向に対する依存性が驚くほど似ていることがわかった（図4、左）。 多様な粒状媒体に対する抵抗力理論の一般性とその実用的な利点

このことは大きな実用的な利点をもたらす。 これらの粒状媒体は一般的な応力プロファイルが同じであるため、最大垂直力を決定するためのたった1回の力測定で、他の方向や向きの力をすべて測定することなく推測できる（図4、右）。 これは、市販のペネトロメーターで簡単に行うことができる。 このことは、テラメカニカル研究で得られた水平板ペネトレーションによる下方向への測定が、抵抗力理論を使ってより強力に利用できることも意味している。

最後に、重ね合わせ原理により、我々の抵抗力理論は原理的に任意の形態や運動様式の動物や装置（低速、非慣性、連続領域で作動すると仮定）に適用可能である。 例えば、水平面内の抵抗力計測を用いた理論が、粒状媒体内でのサンドフィッシュトカゲの動きを予測できることも発見した。

古典的テラメカニクスが火星探査機で失敗する理由

古典的テラメカニクスでは、大きな車輪やトラックは通常、比較的平らで水平な地表面を持っているので、粒状媒体の垂直侵入力は水平板を（ペネトロメータを使って）下方に移動するだけで特徴づけられる（図5）、他の方向や向きの侵入物にはあてはまらないとされています。 これを用いて揚力を予測し、その揚力と車両重量を（静的・動的に）バランスさせて沈下量を予測する

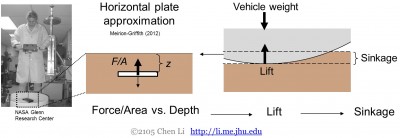
図5. 古典的なテラメカニカルモデルの開発で一般的な水平板近似。

しかし、緩い粒状媒体上を移動するローバーの小さな車輪（または十分に深く沈んだ大きな車輪）については、地面界面は水平から遠く離れた方向で非常に湾曲するようになる。 私たちがすべての方向と向きを考慮した抵抗力測定で示したように、一般に水平な板は水平から遠い板よりはるかに大きな垂直力を受けます（図2左）。 その結果、水平板近似はもはや適用されず、古典的なテラメカニカルモデルは揚力を大幅に過剰に予測し、沈下を過小に予測することになる。 A terradynamics of legged locomotion on granular media, Science, 339, 1408-1412 (Featured in Science Perspective) PDF

.