フリードマンの検定／順位による二元配置分析

Written by on in Articles
Share on

統計の定義 > Friedmanの検定

Friedmanの検定とは？

Friedman の検定は複数の試みにおける処理の差を見つけるためのノンパラメトリック検定である。 ノンパラメトリックとは、データが特定の分布（正規分布など）から来ていることを仮定しない検定であることを意味します。 基本的には、データの分布がわからないときにANOVA検定の代わりに使用される。


Friedmanの検定は符号検定の拡張であり、複数の処理があるときに使用する。

検定の実行

データは次の要件を満たすべきである。 Likertスケール）または連続であること、

  • Data comes from a single group, measured on at least three different occasions,
  • The sample was created with a random sampling method,
  • Block are mutually independent (i.).(すなわち、すべてのペアが独立しており、一方が他方に影響しない),
  • Observations are ranked within blocks with no ties.

    • The null hypothesis for the test is that the treatment all have identical effects, or that the sample differ in some way.

    The null hypothesis for the test is that the treatment all have identical effects, or the sample differ in some way.All rights reserved. 例えば、それらは中心、広がり、または形状が異なる。 対立仮説は、処置が異なる効果を持つというものである。

    検定のためにデータを準備する。

    ステップ1：データをブロック（表計算ソフトの列）に並べ替える（この例では、12人の患者が3種類の治療を受けている）。 ここでは行を越えて順位をつけているので、各患者は各治療に対して1、2、3の順位をつけられています。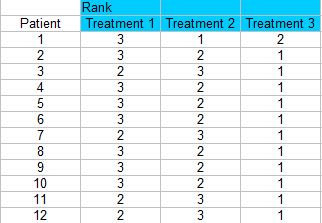
    friedman test 2
    Step 3: 順位を合計する（各列の合計を求める）。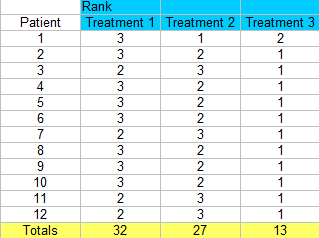
    friedman test 3

    検定を実行する

    注意：この検定は計算に時間がかかり手間がかかるので、通常は手で実行することはない。 ほとんどすべての一般的な統計ソフト・パッケージはこのテストを実行できる。

    ステップ 4: 検定統計量を計算する。 必要なもの：

    1. n: 被験者の数 (12)
    2. k: 処置の数 (3)
    3. R: 3列のそれぞれの総ランク (32, 27, 13)です。

    これらを次の式に挿入して解く：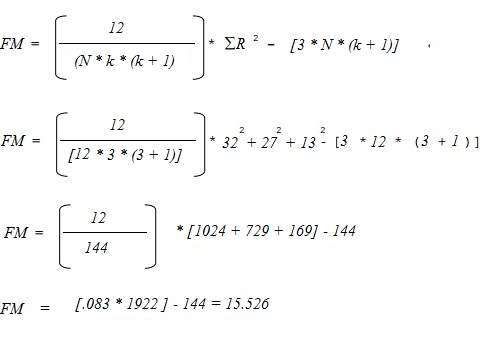
    friedman calculations 1

    Step 5: FM critical value from the table of critical values for Friedman (see below table).
    k=3 table (as it is how many treatments we have) and the alpha level of 5%を使用する。 より高いまたは低いアルファ・レベルを選ぶことができますが、5%はかなり一般的です – なので、アルファ・レベルがわからない場合は、5%の表を使用してください。


    その表でn-12を調べると、FM臨界値は6.17となる。

    ステップ6：計算したFM検定統計量（ステップ4）とFM臨界値（ステップ5）を比較します。 計算されたF値がFM臨界値より大きければ帰無仮説を棄却する。:

    • Calculated FM Test Statistic = 15.526.
    • FM Critical value from table = 6.17.FM Critical value from table = 6.17.FM Test Statistic = 15.526.
    • FM Critical value from table = 6.17.

    計算したFM統計量の方が大きいので、帰無仮説を棄却する。

    Friedman’s ANOVA by Ranks Critical Value Table

    kによる3つのテーブル。
    k が5以上、または n が13以上の場合、ステップ5のカイ二乗臨界値表で臨界値を求めます。

    k=3

    6.00

    <.05 – <-

    N α<.10 α ≦.05 α <.01
    3 –
    4 6.00 – 4 6.006.00 6.50 8.00
    5 5.20 6.40 8.40
    6 5.33 7.00 9.00
    7 5.43 7.14 8.86
    8 5.25 6.25 9.00
    9 5.56 6.22 8.67
    10 5.00 6.20 9.60
    11 4.91 6.54 8.91
    12 5.17 6.17 8.67
    13 4.77 6.00 9.39
    ∞ 4.61 5.99 9.21

    k=636>

    N

    <.01

    6.00

    α7924>.10 α ≦.05
    2 –
    3 6.00 6.00 6.00 6.00> 8.00> 8.00> 9.00 9.0060 7.40 8.60
    4 6.30 7.80 9.60
    5 6.36 7.80 9.96
    6 6.40 7.60 10.00
    7 6.26 7.80 10.37
    8 6.30 7.50 10.35
    ∞ 6.25 7.82 11.34

    k=4

    N α<.10 α ≦.05 α <.01
    3 7.47 8.53 10.13
    4 7.60 8.80 11.00 5 7.68 8.96 11.52 ∞ 7.78 9.49 13.28

    参考：
    フリードマンの順位別二元配置分析-
    量的応答変数を用いたk-グループ内データの分析. Retrieved 7-17-2016 from: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF

    CITE THIS AS:
    Stephanie Glen. “フリードマンの検定/順位による二元分散分析” StatisticsHowTo.comより。 私たちのための初歩的な統計学 https://www.statisticshowto.com/friedmans-test/

    ————————————————————–

    宿題やテストの質問で助けが必要ですか？ Chegg Studyでは、その分野の専門家からステップバイステップの解決策を得ることができます。 Cheggのチューターとの最初の30分間は無料です!

    コメントを残す

    メールアドレスが公開されることはありません。