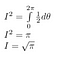ケルビン公はこの積分をこう記したそうです。 “A mathematician is one to which is as obvious as that twice two makes four is to you.”
お楽しみに 😉
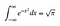
さて、あなたが積分と微分について基本を知っているという前提でお話させて頂きますね。 以下は、後に出てくる巧妙なトリックに直感を加えるものです。 多少不可解な点があっても気にせず、何が起こっているのかを感じ取るようにしましょう。
ここでの戦略は、巧妙な代入をすることです。 しかし、私たちは 2 つの変数で代入を行います。 今の問題は、曲線の下の面積を計算するものとしてイメージできます
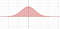
しかし、この問題は体積を計算するものに変えることができることを紹介します。
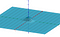
体積を計算するには、通常の積分とは少し異なる変数変換の公式を使用します。 ここでは、極座標を使います。 これは、xとyの座標を半径と角度で表現します。 Geogebra には、これをインタラクティブに表示する方法があります

では、極座標の魔法のような基底の変更式を使用します。
曲線下の面積を計算するとき、x 軸に沿って小さな距離を表す要素 ‘dx’ を持ちました。 体積を計算するときは、dx dy という要素があって、これは辺の長さが dx と dy の小さな直方体のようなものです。 そして、これらの底辺を利用して、体積を推定する一連のボックスを作成する。 これは、下の図が一番わかりやすい。 積分はこれらの近似の限界です。
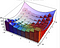
代わりに極座標系を使うと、その下の面積要素は少し違ってきます。 下の、dAが面積要素です。 角度と半径を少し変えると、この面積要素は次第に、それぞれ辺の長さが dr と r*dtheta の長方形で近似されるようになります。 もしあなたがある程度の幾何学に慣れているなら、小さなtheta sin(theta)はthetaで非常によく近似され、その後以下の結果を証明できます。
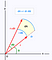
Solving the integral
まず、私たちは積分に名前をつけます。 それをIと呼びます。
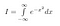
xは単なる「ダミー変数」であることに注意しましょう。 どのような変数名を使っても領域は存在する。 ですから、次の2つの式
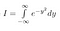
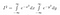
ここで、Iは値が分からないとはいえ単なる定数にすぎないから、Iの値が分からないとします。
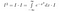
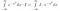
ここまであまり大したことはないのですけれども、この辺で。 ここで、積分の意味についてしっかり考えてみましょう。 私たちは関数の積分をとります。 2つの関数がどこでも同じ値をとれば、同じであり、同じ面積を持つ。 それを念頭に置いて、I*exp(-x²)をxの関数、つまり入力としてxの値を取り込み、出力として数値を与えるものと見なすと、次のような操作ができます。
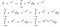
OK, それは大変だったね。 1行目では、Iを変数名を変えて積分形に書き換えただけです。 2行目では、I*exp(-x²)を関数として扱い、dy積分の内部にexp(-x²)を持ち込むことができ、これはxのどの入力値に対してもまだ同じ出力値を与えることに気づきました。
これを完全に書き出すと、
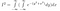
次は、キラーインサイトが来るぞ。 上では、変数名と関数の表現方法をいじくりまわしてきました。 今、私たちは視点を変えます。この式はまた、面積要素 dA = dx dy で、2D 平面全体にわたる exp(-(y²+x²)) の積分を表します。 つまり、dx dy は平面上の小さな長方形で、exp(-(y²+x²)) はその長方形の上の高さです。
次に、先ほどの極座標の洞察
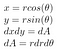
sin² + cos² = 1として、すべてを差し込むと、以下のようになります。 となり、
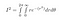
r は 0 から無限大、theta は 0 から 2*pi まで、これは2次元平面全体をカバーするからである。 どの点も半径は無限大より小さく、角度は0から2πラジアンの間にある。
鎖の法則
を使って内積分を評価することができる。
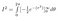
そして、私たちは今約束の地にいる。