電荷と電場についてはほとんど知っているが、ガウスの法則についてはどうだろうか？ ガウス則はこの章の重要なトピックですが、ガウス則に入る前に、ガウス面とは何か、どのようにガウス面を決定するのかを理解する必要があります。
ガウス面を決定する方法について進む前に、まずガウス面とは何かについて理解しましょう。

ガウス曲面とは 電界（E）と面積ベクトル（A）のなす角（ө）がどの点でも常に一定である曲面、これがガウス曲面です。
ベクトルには大きさと方向がありますから、面積ベクトルは平面のベクトルで、大きさは表面の面積、方向は表面に垂直な方向です。

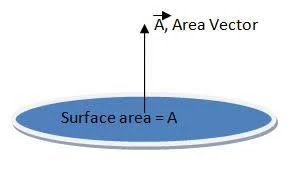
面積ベクトル

さて、ガウス面を見たらどう識別するのでしょう。

ガウス面の求め方

ガウス面はガウスの法則に従っており、電界(E)と面積ベクトル(A)のなす角(ө)は各点で常に同じであることが分かっています。 したがって、ガウス面を決定するには、面上の各点で角度(ө)が同じかどうかを調べればよいのです。
ガウスの法則。

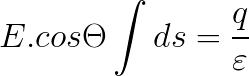
以下はガウス面の決定手順です。
ステップ1：物体またはオブジェクトから表面を選択する
そこでしばしば人々は混乱し、物体上のすべての点の角度が同じかどうかを確認し始めます。 しかし、ここではっきりさせておきたいのは、物体上の表面がガウス面であるかどうかを識別したいのであって、物体全体の各点ではなく、表面上の各点で角度（ө）をチェックしたいのだということです。

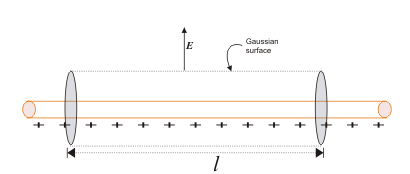
面の識別

上の画像では、物体内の面がガウス面かどうかを調べるために、影のない領域を考慮し、影のある領域は考慮しないようにしているのです。
P.s.: 1つの物体が複数のガウス面を持つことができることを意味します。
ステップ2：電界の方向を調べる
次に、表面を決めたら、その表面から電界がどの方向に出ているかを調べます。

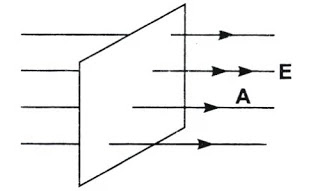
電界方向

電界や電界線について分からない場合は、別の記事で電界とガウス面の導出と法則を手書きでメモしましたから、そちらを読んでみてください。 ここをクリック
ステップ3: 面積ベクトルを求める
電界の向きを求めたら、次は面の面積ベクトルを求めます。 面積ベクトルとは、表面に対して常に垂直な方向を持つベクトルです。
ステップ4: 面積ベクトル(A)と電界(E)のなす角を調べる
電界と面積ベクトルの方向がわかったら、次はそのなす角(ө)を調べましょう。

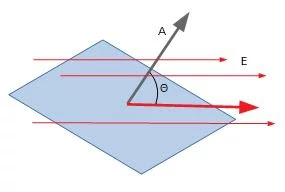
面積ベクトルと電場の角度

両者の角度がすべての点で同じかどうかを確認する。

なぜガウス曲面を求める必要があるのでしょうか。

ガウス曲面は、異なる電荷分布による電場の評価に役立ちます。
異なる電荷分布による電場の評価について知りたい場合は、このサイトに私のメモがアップロードされています。

Some examples of Gaussian surface:

そこで、ガウス曲面の例として、以下のものを挙げます。
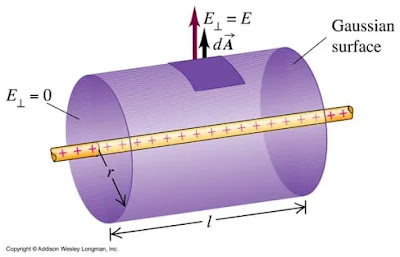
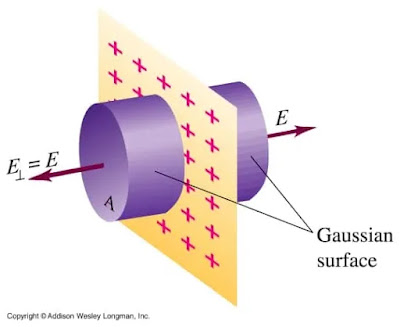
1. 1. 直線帯電導体による電界を求めるために作成した虚数円柱のガウス曲面。 この導出はノートに書いてあります:)

2. 平面帯電シートによる電界を求めるために作られた虚円筒形のガウス曲面。 この導出もノートに書いてあります 🙂