イジング模型は熱力学系の特殊な例であり、相転移を理解するためのモデル系です。 多くの生物学者が、わずかなミバエに多くの時間を費やしているのをご存じでしょうか。 物理学者はイジング模型に多くの時間を費やしているのです。

個人的には、ミバエは気持ち悪いと思うので、彼の例えが一番好きではありません。

Motivation

なぜ私たちはイジングモデルの話に多くの時間を費やす必要があるのでしょうか。

• 相転移に関するあらゆる種類の動作について考えるのに驚くほど便利です。 たとえば、

  • イジング模型は低温相で対称性の破れを示します（先ほどお話したとおりです）

  • よく定義された温度で特別な「臨界点」を持ちます（水の相図で言及しました）

  • その他の特徴も豊富です。

• 熱力学的な量を実際に計算して解釈することができる、正確に解ける数少ないモデルの一つです。

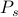  • 一般に、熱力学量の計算は多くの項の合計をしなければならないので大変です。 最初の熱力学の授業で、平衡系を多くの状態のアンサンブルとして考えることができ、それぞれが独自の確率で重みづけされていることを思い出してください。 この枠組みでは、観測される熱力学量はアンサンブルの平均に相当する。 特に、ある観測値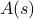のアンサンブル平均を求める場合、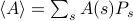を求める必要があり、ここで和はすべての可能な状態について計算されます。 この場合の問題は、熱力学系の状態数が粒子の数に対して指数関数的に増加することです。 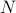が 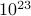のオーダーである熱力学系はともかく、中程度の大きさの系でもコンピュータが明示的に平均を計算するには状態が多すぎます。

  • だから分割関数を計算するには「賢く」なければならず、正確に解ける系に感謝しなければならないのです!

• イジングモデルは単純ですが、驚くほど多くの異なる系に適用できます。

  • これは普遍性の最初の味です。 物理学者は、このような一般的な振る舞いが、混沌とした世界におけるより深い秩序を示唆するので、大好きなのです。 それはサイトの巨大な（正方形の）格子で、各サイトは2つの状態のうちの1つになることができます。 各サイトにというインデックスをつけ、との2つの状態を呼びます。 7740>番目のサイトがの状態にあると言うためには、 .

    

    さて、この定義はひどく抽象的で物理的でないので、 我々物理屋にとっては、実際のシステムを念頭に置いて、 何か明示的に言及したり物理的直観を構築できることが非常に助かる。 イジングモデルが表現する可能性のある物理系をいくつか挙げてみます：

    • 磁石。 各サイトは物質中の特定の「スピン」（不対電子？）を表し、スピンが下を向いていれば、上を向いていればである。 各スピンは、それ自身の小さな磁気モーメントを持つ小さな磁石のように動作します。すべてのスピンが整列している場合、スピンの全体の格子は、正味の巨視的磁気モーメントを持つ大きな磁石のように動作します。 はそのサイトの銅原子を表し、 は亜鉛を表します。

    • ”格子ガス”。 各サイトは粒子の存在しうる場所であり、はそのサイトが空であることを、はそのサイトが粒子によって占有されていることを意味する。

    • Bacterial vortex lattices???

    今はイジングモデルを磁石に対するモデルとして考えることにしよう。

    Putting together the Hamiltonian

    このミッキーマウスのような磁石のモデルについて、当然の疑問は、それがどのようなエネルギーを持っているかということです。 正確には、磁石の中のスピンの配置（微小状態）のエネルギーを表す関数を書き下ろしたいのです。 ご存知のように、このエネルギー関数はハミルトニアンと呼ばれます。

    イジング模型では、ハミルトニアンは2種類の相互作用を含んでいます。 量子力学で習ったように、外部磁場はスピンダウンとスピンアップのエネルギーを分けることができ、一方はエネルギーが高く、他方は低くなります。

    • のサイズは磁場の強さを表しているので、一方のスピンが他方よりどれだけエネルギーが高いかが分かります。

    • の符号でスピンアップとスピンダウンどちらか好きかが分かります。

    • 個々のスピンが外場を感じているので、エネルギーへの貢献の合計を見つけるために、すべてのサイトを合計する必要があります。

    • 隣接するスピン間の相互作用項 – 互いに整合して同じ方向に向けたい、あるいは反対に整合して異なる方向に向けたい。 物理的には、磁石内の各スピンはそれ自身の磁場を設定する小型磁気双極子であり、隣接するスピンはその磁場を感じることができるので、この相互作用が発生すると想像することができます。

      • の大きさは、隣り合うスピンがどれだけ強く結合しているか、つまりどれだけ（反）並びたがっているかを示しているのです。

      • の符号は、隣接するスピンが揃えたいか反揃えたいかを教えてくれます。 (専門用語では、それぞれ強磁性、反強磁性です）。 物理的には、物質がどちらか一方であるか（あるいはどちらでもないか）は、スピンがどのように相互作用するかの正確な量子力学的詳細に依存します。

      • スピン-スピン相互作用は2つのスピン間で発生するので、エネルギーに対するその総相互作用を見つけるためにサイトのペアで合計する必要があります。

      相互作用項の詳細

      スピン-スピン相互作用項に関する自然な疑問は、どのスピンがどのスピンと結合しているかということです。

      再び磁石の物理的な絵に戻り、ある特定のスピンにズームインすると、スピン-スピン相互作用の強さは近くのスピンで強く、遠くのスピンで弱くなると予想されます。

      イジングモデルの場合、このスピン-スピン相互作用の性質について、最も単純な仮定をします：

      Nearest-neighbor interaction

      イジングモデルでは、各格子サイトは、格子上でそれに直接隣接するサイトとのみ相互作用します。

      いくつかのコメント：

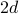      • 次元の正方格子では、各サイトは近傍を持ちます：1次元では左と右、2次元を追加すると上と下、など。

      • 我々は、等方性の相互作用を仮定します – 方向に関係なくすべての隣接が平等に扱われます。

      • 我々はしばしば最近傍相互作用について、2つの格子サイトを結合する結合のエネルギーとして話します。

      • 隣接するサイトのペアについて合計するとき、記号的に、インデックスの周りに小さな角括弧を書いて、「最近接」を表します。

      最近接相互作用の良い結果は、あるスピンの配置について合計エネルギーを求めるとき、サイトの可能なすべてのペアについて合計するのではなく、互いに隣接したサイトのペアにのみ合計することにあるということです。

      備考

      もちろん、より複雑で現実的なモデルでは、これらの仮定のいくつかを緩和して、長距離相互作用や非等方的相互作用を許容するかもしれませんが、今のところ、これは我々が考え得る最も単純な相互作用であり、これを大切にして、これが我々に何を教えてくれるかを見るべきでしょう!

      さて、これらのことを議論したので、ハミルトニアンの実際の式を書き下す準備ができました。 (ハミルトニアンを書き出す前に物理の説明と解釈をして、記号がなんとなくわかるようにしたかったのです。)

      イジングモデルのハミルトニアン

      イジングモデルのハミルトニアンは、

      

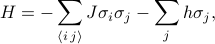
      ここではスピン-スピン相互作用を、は外場、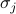は格子サイトごとのスピンを表しています。 最初の和は隣接する格子サイト(ボンド)の全ペアで、スピン間の相互作用を表しています。 2つ目の和は、すべての格子サイト自身に関するもので、すべてのスピンを1つの方向に整列させようとする外的な場を表します。