La varianza è un numero che indica quanto distano un insieme di numeri. La varianza è identica alla deviazione standard al quadrato e quindi esprime “la stessa cosa” (ma più fortemente).
Varianza – Esempio
Uno studio fa eseguire a 100 persone un semplice compito di velocità durante 80 prove. Per ogni partecipante, vengono così registrati 80 tempi di reazione (in secondi). Una parte di questi dati è mostrata qui sotto.

In studi come questi, vediamo tipicamente che le persone diventano più veloci man mano che eseguono il compito di velocità più spesso. Cioè, il tempo medio di reazione tende a diminuire nel corso delle prove.
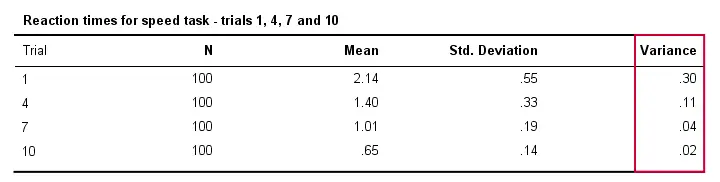
Inoltre, i tempi di reazione tipicamente variano meno tra persone diverse nella misura in cui eseguono il compito più spesso. Tecnicamente, diciamo che la varianza diminuisce con le prove. La tabella qui sotto illustra questo per le prove 1,4,7 e 10.
Varianza e Istogramma
Un ottimo modo per visualizzare i dati della nostra tabella precedente è un istogramma per ogni prova. Così, la figura qui sotto illustra che i partecipanti sono diventati più veloci nel corso delle prove; dalla prova 1 alla prova 10 le barre dell’istogramma si spostano verso sinistra, verso 0 secondi.
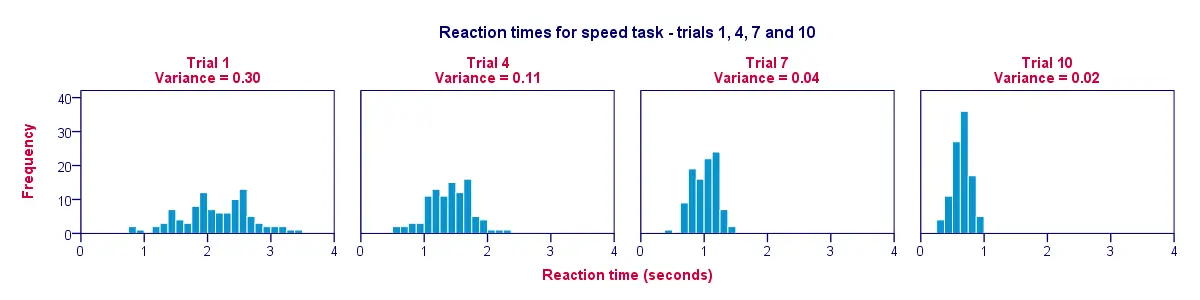
Un secondo risultato è che gli istogrammi diventano più stretti (e quindi più alti) mentre ci spostiamo dalla prova 1 alla prova 10; questo illustra che i tempi di reazione variano sempre meno tra i nostri partecipanti mentre l’esperimento procede. La varianza diminuisce nel corso delle prove.
Formula della varianza – Popolazione
Una formula di base per calcolare la varianza è
$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$
Si consiglia di cercare di capire cosa fa questa formula perché aiuta molto a capire l’ANOVA (= analisi della varianza). Lo dimostreremo quindi su una semplice manciata di dati.
Varianza – GoogleSheets
Per semplicità, ridurremo i nostri dati alla prima prova per i primi 5 partecipanti. Questi 5 tempi di reazione – e un calcolo manuale della loro varianza – sono in questo GoogleSheet.
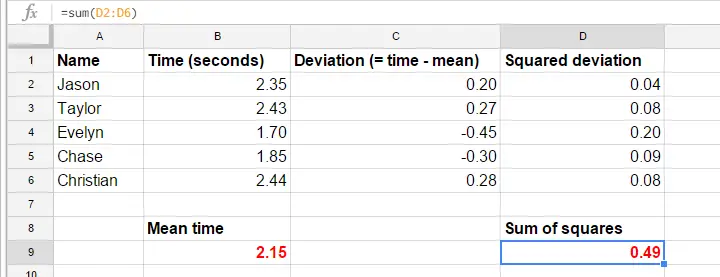
Varianza – Passi di calcolo
Le formule nel GoogleSheet mostrano esattamente come calcolare una varianza. I passi fondamentali sono
- calcolare il tempo medio di reazione (2,15);
- calcolare i punteggi di deviazione (tempo di reazione meno tempo medio di reazione);
- calcolare i punteggi di deviazione al quadrato;
- aggiungere i punteggi di deviazione al quadrato. Il risultato (0,49) è una somma dei quadrati, il blocco principale dell’ANOVA;
- dividete la somma dei quadrati per il numero di osservazioni (5 tempi di reazione).
In alternativa, calcolate una varianza digitando =VARP(B2:B6) in qualche cella (B2:B6 sono le celle che contengono i nostri 5 tempi di reazione). VARP è l’abbreviazione di “varianza della popolazione”. OpenOffice e MS Excel contengono formule simili.
Varianza – Formula campione
Similmente alla deviazione standard, se i nostri dati sono un semplice campione casuale da una popolazione molto più grande, la formula di cui sopra sottostimerà sistematicamente la varianza della popolazione. In questo caso useremo una formula leggermente diversa:
$$S^2 = \frac{\somma(X_i – \overline{X})^2}{n – 1}$$
Quale formula usare dipende quindi dai nostri dati: contengono l’intera popolazione che vogliamo studiare o sono un semplice campione di questa popolazione? In GoogleSheets, digitando =VAR(B2:B6) in qualche cella si ottiene la varianza del campione.
Varianza in SPSS
Per quanto ne sappiamo, la formula per la varianza della popolazione è completamente assente in SPSS e lo consideriamo un grave difetto. Invece, SPSS usa sempre la formula del campione, sia per la varianza tra soggetti (discussa in questo tutorial) che per la varianza tra soggetti. L’output rilevante è mostrato qui sotto.

Per quanto riguarda questa tabella di output, notate anche che la varianza è effettivamente la deviazione standard al quadrato (a parte l’arrotondamento).
Per quanto riguarda la varianza, questo è tutto. Speriamo che questo tutorial ti sia stato utile per capire cos’è la varianza.