Quanto sai degli infiniti? Probabilmente hai sentito parlare di un numero che è il più grande numero possibile, o impossibilmente grande.
Per spiegare gli infiniti, devo prima definire un po’ di terminologia.
Gli interi sono numeri usati per contare. L’insieme degli interi è definito come tutti i numeri senza componenti frazionarie. Alcuni esempi sono: -12, 0, 1, 3, 42, 17.
L’infinito è il concetto di un oggetto oltre la portata dei numeri naturali. Fu concettualizzato per la prima volta da un matematico russo di nome Georg Cantor, che non solo introdusse l’infinito, ma rivelò anche che esistevano più infiniti.
Cantor fornì una prova controversa degli infiniti, che diceva che alcuni infiniti erano più grandi di altri. All’inizio, questo può sembrare impossibile: come può un oggetto essere più grande di un altro oggetto che è infinito?

Cantor basò la sua prova su un ramo della matematica che è apparentemente inutile: La teoria degli insiemi. Un insieme è una collezione di oggetti – per esempio, possiamo avere un insieme contenente 1, 2 e 3. Questi oggetti nell’insieme sono chiamati elementi.
In notazione matematica, questo sarebbe come:
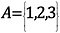
Il numero di elementi in questo insieme, o la cardinalità dell’insieme, è 3.
Questo è indicato come:
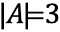
Se ora abbiamo un altro insieme, B, contenente oggetti, tale che
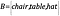
Come sappiamo che gli insiemi hanno la stessa dimensione?
Un modo per vederlo è contare il numero di elementi nel secondo insieme. Possiamo vedere chiaramente che anche questo insieme ha 3 elementi, e quindi sappiamo che hanno la stessa dimensione.
Un altro modo in cui possiamo farlo è confrontando il nostro secondo insieme, B, con il nostro primo insieme, A, tramite mappatura.
Possiamo mappare il primo elemento dell’insieme A, 1, al primo elemento dell’insieme B, sedia.
Possiamo mappare il secondo elemento dall’insieme A, 2, al secondo elemento dell’insieme B, tavolo.
Possiamo mappare il terzo elemento dall’insieme A, 3, al terzo elemento dell’insieme B, cappello.
Siccome ogni elemento di A è mappato su esattamente 1 elemento di B, gli insiemi hanno dimensioni uguali.
Diamo ora uno sguardo agli insiemi infiniti. L’insieme dei numeri interi, che è stato menzionato all’inizio, è un insieme infinito – ci sono un numero infinito di numeri interi. L’insieme dei numeri interi è indicato con il simbolo
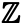
L’insieme dei numeri pari, che possiamo indicare come

è definito come
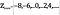
Intuitivamente, può sembrare
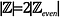
che ci siano 2 interi per ogni intero pari: 1 intero dispari e 1 intero pari. Verifichiamo questo.
Proviamo a confrontare gli insiemi mappando gli elementi da un insieme all’altro.
Possiamo mappare 1 a 2, 2 a 4, 3 a 6, e così via.
Se questo continua per tutti gli insiemi, possiamo vedere che ogni elemento dell’insieme intero mappa esattamente 1 elemento dell’insieme intero pari.
Quindi, anche se può sembrare controintuitivo, le dimensioni degli insiemi sono uguali.