La convoluzione indesiderata è un problema inerente al trasferimento di informazioni analogiche. Per esempio, tutto ciò che segue può essere modellato come una convoluzione: sfocatura dell’immagine in una macchina fotografica traballante, echi nelle chiamate telefoniche a lunga distanza, la larghezza di banda infinita dei sensori analogici e dell’elettronica, ecc. La deconvoluzione è il processo di filtraggio di un segnale per compensare una convoluzione indesiderata. L’obiettivo della deconvoluzione è di ricreare il segnale come esisteva prima che la deconvoluzione avesse luogo. Questo di solito richiede che le caratteristiche della convoluzione (cioè, la risposta all’impulso o alla frequenza) siano note. Questo può essere distinto dalla deconvoluzione cieca, dove le caratteristiche della convoluzione parassita non sono note. La deconvoluzione cieca è un problema molto più difficile che non ha una soluzione generale, e l’approccio deve essere adattato all’applicazione particolare.
La deconvoluzione è quasi impossibile da capire nel dominio del tempo, ma molto semplice nel dominio della frequenza. Ogni sinusoide che compone il segnale originale può essere cambiata in ampiezza e/o fase mentre passa attraverso la convoluzione indesiderata. Per estrarre il segnale originale, il filtro di deconvoluzione deve annullare questi cambiamenti di ampiezza e fase. Per
esempio, se la convoluzione cambia l’ampiezza di una sinusoide di 0,5 con uno spostamento di fase di 30 gradi, il filtro di deconvoluzione deve amplificare la sinusoide di 2,0 con un cambiamento di fase di -30 gradi. Come illustrato nella Fig. 17-3, questo dispositivo è composto da due parti, uno scintillatore e un rilevatore di luce. Uno scintillatore è un tipo speciale di materiale trasparente, come lo ioduro di sodio o il germanato di bismuto. Questi composti cambiano l’energia di ogni raggio gamma in un breve scoppio di luce visibile. Questa luce
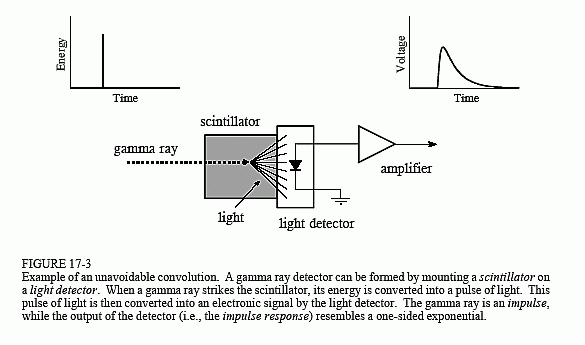
viene poi convertita in un segnale elettronico da un rilevatore di luce, come un fotodiodo o un tubo fotomoltiplicatore. Ogni impulso prodotto dal rivelatore assomiglia a un esponenziale unilaterale, con qualche arrotondamento degli angoli. Questa forma è determinata dalle caratteristiche dello scintillatore utilizzato. Quando un raggio gamma deposita la sua energia nello scintillatore, gli atomi vicini sono eccitati ad un livello di energia superiore. Questi atomi si deeccitano in modo casuale, ciascuno producendo un singolo fotone di luce visibile. Il risultato netto è un impulso di luce la cui ampiezza decade in poche centinaia di nanosecondi (per lo ioduro di sodio). Poiché l’arrivo di ogni raggio gamma è un impulso, l’impulso in uscita dal rivelatore (cioè l’esponenziale unilaterale) è la risposta all’impulso del sistema.
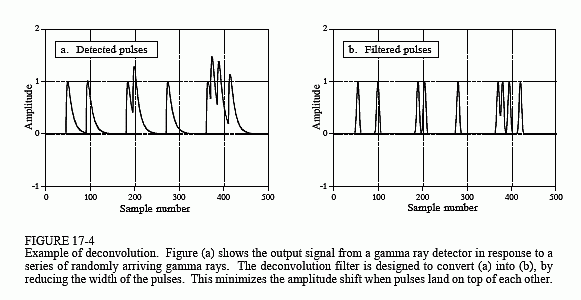
La figura 17-4a mostra gli impulsi generati dal rivelatore in risposta ai raggi gamma che arrivano in modo casuale. L’informazione che vorremmo estrarre da questo segnale di uscita è l’ampiezza di ogni impulso, che è proporzionale all’energia del raggio gamma che lo ha generato. Questa è un’informazione utile perché l’energia può dire cose interessanti su dove il raggio gamma è stato. Per esempio, può fornire informazioni mediche su un paziente, dire l’età di una galassia lontana, rilevare una bomba nel bagaglio aereo, ecc.
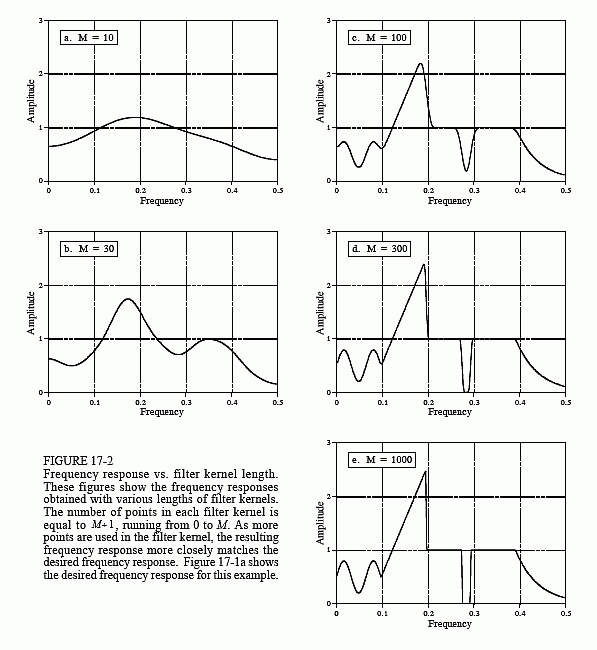
Tutto andrebbe bene se solo un occasionale raggio gamma venisse rilevato, ma questo di solito non è il caso. Come mostrato in (a), due o più impulsi possono sovrapporsi, spostando l’ampiezza misurata. Una risposta a questo problema è quella di deconvolvere il segnale di uscita del rivelatore, rendendo gli impulsi più stretti in modo che si verifichi meno pile-up. Idealmente, vorremmo che ogni impulso assomigliasse all’impulso originale. Come si può sospettare, questo non è possibile e dobbiamo accontentarci di un impulso di lunghezza finita, ma significativamente più breve dell’impulso rilevato. Questo obiettivo è illustrato nella figura 17-4b.
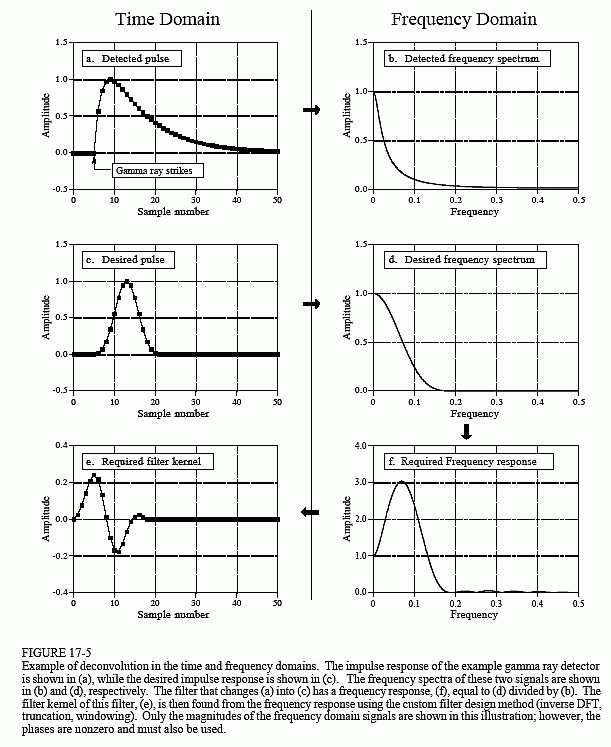
Anche se il segnale del rivelatore ha le sue informazioni codificate nel dominio del tempo, gran parte della nostra analisi deve essere fatta nel dominio della frequenza, dove il problema è più facile da capire. La figura 17-5a è il segnale prodotto dal rivelatore (qualcosa che conosciamo). La figura (c) è il segnale che vorremmo avere (anch’esso qualcosa che conosciamo). Questo impulso desiderato è stato arbitrariamente selezionato per avere la stessa forma di una finestra di Blackman, con una lunghezza di circa un terzo di quella dell’impulso originale. Il nostro obiettivo è quello di trovare un kernel di filtro, (e), che quando è convoluto con il segnale in (a), produce il segnale in (c). In forma di equazione: se a * e = c, e dati a e c, trovae.
Se questi segnali fossero combinati per addizione o moltiplicazione invece che per convoluzione, la soluzione sarebbe facile: la sottrazione è usata per “de-aggiungere” e la divisione per “de-moltiplicare”. La convoluzione è diversa; non c’è una semplice operazione inversa che possa essere chiamata “deconvoluzione”. La convoluzione è troppo disordinata per essere annullata manipolando direttamente i segnali nel dominio del tempo.
Per fortuna, questo problema è più semplice nel dominio della frequenza. Ricordate, la convoluzione in un dominio corrisponde alla moltiplicazione nell’altro dominio. Sempre riferendoci ai segnali in Fig. 17-5: se b × f = d, e dati b e d, trovate f. Questo è un problema facile da risolvere: la risposta in frequenza del filtro, (f), è lo spettro di frequenza dell’impulso desiderato, (d), diviso per lo spettro di frequenza dell’impulso rilevato, (b). Poiché l’impulso rilevato è asimmetrico, avrà una fase non nulla. Questo significa che si deve usare una divisione complessa (cioè una fase di magnitudine & divisa per un’altra fase di magnitudine &). Nel caso l’abbiate dimenticato, il capitolo 9 definisce come eseguire una divisione complessa di uno spettro per un altro. Il kernel del filtro richiesto, (e), viene quindi trovato dalla risposta in frequenza con il metodo del filtro personalizzato (IDFT, shift, truncate, &moltiplica per una finestra).
Ci sono limiti al miglioramento che la deconvoluzione può fornire. In altre parole, se si diventa avidi, le cose crollano. Diventare avidi in questo esempio significa cercare di rendere l’impulso desiderato eccessivamente stretto. Guardiamo cosa succede. Se l’impulso desiderato è reso più stretto, il suo spettro di frequenza deve contenere più componenti ad alta frequenza. Poiché queste componenti ad alta frequenza sono ad un’ampiezza molto bassa nell’impulso rilevato, il filtro deve avere un guadagno molto alto a queste frequenze. Per esempio, (f) mostra che alcune frequenze devono essere moltiplicate per un fattore di tre per ottenere l’impulso desiderato in (c). Se l’impulso desiderato è reso più stretto, il guadagno del filtro di deconvoluzione sarà ancora maggiore alle alte frequenze.
Il problema è che i piccoli errori non perdonano in questa situazione. Per esempio, se qualche frequenza è amplificata di 30, quando solo 28 è richiesto, il segnale deconvoluto sarà probabilmente un casino. Quando la deconvoluzione viene spinta a maggiori livelli di prestazioni, le caratteristiche della convoluzione indesiderata devono essere comprese con maggiore accuratezza e precisione. Ci sono sempre incognite nelle applicazioni del mondo reale, causate da tali cattivi come: rumore elettronico, deriva della temperatura, variazione tra dispositivi, ecc. Queste incognite pongono un limite al funzionamento della deconvoluzione.
Anche se la convoluzione indesiderata è perfettamente compresa, c’è ancora un fatto che limita le prestazioni della deconvoluzione: il rumore. Per esempio, la maggior parte delle convoluzioni indesiderate prende la forma di un filtro passa-basso, riducendo l’ampiezza delle componenti ad alta frequenza nel segnale. La deconvoluzione corregge questo amplificando queste frequenze. Tuttavia, se l’ampiezza di queste componenti cade sotto il rumore intrinseco del sistema, l’informazione contenuta in queste frequenze è persa. Nessuna quantità di elaborazione del segnale può recuperarla. È andato per sempre. Adios! Addio! Sayonara! Cercare di recuperare questi dati non farà che amplificare il rumore. Come caso estremo, l’ampiezza di alcune frequenze può essere completamente ridotta a zero. Questo non solo cancella l’informazione, ma cercherà di far sì che il filtro di deconvoluzione abbia un guadagno infinito su queste frequenze. La soluzione: progettare un filtro di deconvoluzione meno aggressivo e/o porre dei limiti su quanto guadagno è permesso a qualsiasi frequenza.
Quanto lontano si può andare? Quanto avido è troppo avido? Questo dipende totalmente dal problema che si sta attaccando. Se il segnale si comporta bene e ha un basso rumore, probabilmente si può fare un miglioramento significativo (si pensi a un fattore di 5-10). Se il segnale cambia nel tempo, non è particolarmente ben compreso, o è rumoroso, non riuscirete a fare altrettanto bene (pensate a un fattore di 1-2). Una deconvoluzione di successo comporta una grande quantità di test. Se funziona ad un certo livello, provate ad andare oltre; saprete quando cade a pezzi. Nessuna quantità di lavoro teorico vi permetterà di aggirare questo processo iterativo.
La deconvoluzione può anche essere applicata a segnali codificati nel dominio della frequenza. Un esempio classico è il restauro di vecchie registrazioni del famoso cantante d’opera Enrico Caruso (1873-1921). Queste registrazioni sono state fatte con attrezzature molto primitive per gli standard moderni. Il problema più significativo sono le risonanze del lungo corno di registrazione tubolare usato per raccogliere il suono. Ogni volta che il cantante colpisce una di queste frequenze di risonanza, il rumore della registrazione aumenta bruscamente. La deconvoluzione digitale ha migliorato la qualità soggettiva di queste registrazioni
riducendo i punti forti nella musica. Descriveremo solo il metodo generale; per una descrizione dettagliata, vedere l’articolo originale: T. Stockham, T. Cannon, andR. Ingebretsen, “Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.
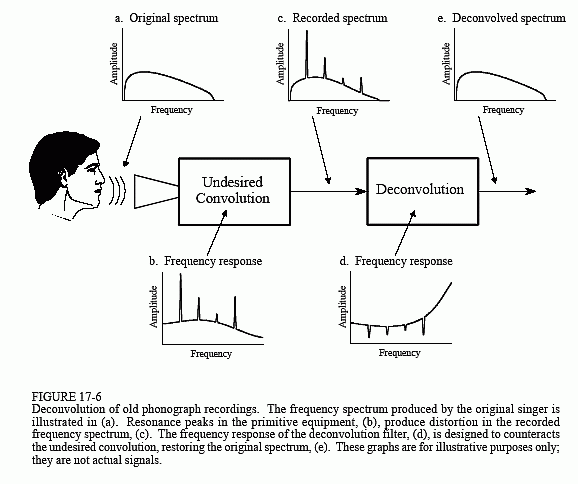
La figura 17-6 mostra l’approccio generale. Lo spettro di frequenza del segnale audio originale è illustrato in (a). La figura (b) mostra la risposta in frequenza dell’apparecchio di registrazione, una curva relativamente liscia eccetto alcuni picchi di risonanza. Lo spettro del segnale registrato, mostrato in (c), è uguale allo spettro vero, (a), moltiplicato per la risposta in frequenza irregolare, (b). L’obiettivo della deconvoluzione è di contrastare la deconvoluzione indesiderata. In altre parole, la risposta in frequenza del filtro di deconvoluzione, (d), deve essere l’inverso di (b). Cioè, ogni picco in (b) è cancellato da una corrispondente diminuzione in (d). Se questo filtro fosse perfettamente progettato, il segnale risultante avrebbe uno spettro, (e), identico a quello dell’originale.
Ecco il problema: l’apparecchio di registrazione originale è stato scartato da tempo, e la sua risposta in frequenza, (b), è un mistero. In altre parole, questo è un problema di deconvoluzione cieca; dato solo (c), come possiamo determinare (d)?
I problemi di deconvoluzione cieca sono di solito attaccati facendo una stima o una supposizione sui parametri sconosciuti. Per trattare questo esempio, si suppone che lo spettro medio della musica originale corrisponda allo spettro medio della stessa musica eseguita da un cantante di oggi con attrezzature moderne. Lo spettro medio si trova con le tecniche del capitolo 9: rompere il segnale in un gran numero di segmenti, prendere la DFT di ogni segmento, convertire in forma polare, e poi fare la media delle grandezze insieme. Nel caso più semplice, la risposta in frequenza sconosciuta viene presa come lo spettro medio della vecchia registrazione, diviso per lo spettro medio della registrazione moderna. (Il metodo usato da Stockham et al. si basa su una tecnica più sofisticata chiamata elaborazione omomorfica, che fornisce una stima migliore delle caratteristiche del sistema di registrazione).