Definizioni di statistica > Test di Friedman
Che cos’è il test di Friedman?
Il test di Friedman è un test non parametrico per trovare differenze nei trattamenti attraverso più tentativi. Non parametrico significa che il test non presuppone che i dati provengano da una particolare distribuzione (come la distribuzione normale). Fondamentalmente, viene usato al posto del test ANOVA quando non si conosce la distribuzione dei dati.
Il test di Friedman è un’estensione del test di segno, usato quando ci sono trattamenti multipli. Infatti, se ci sono solo due trattamenti i due test sono identici.
Eseguire il test
I tuoi dati dovrebbero soddisfare i seguenti requisiti:
- I dati dovrebbero essere ordinali (ad es. la scala Likert) o continui,
- I dati provengono da un unico gruppo, misurati in almeno tre diverse occasioni,
- Il campione è stato creato con un metodo di campionamento casuale,
- I blocchi sono reciprocamente indipendenti (cioè tutte le coppie sono indipendenti).Cioè tutte le coppie sono indipendenti – una non influenza l’altra),
- Le osservazioni sono classificate all’interno dei blocchi senza legami.
L’ipotesi nulla del test è che i trattamenti abbiano tutti effetti identici, o che i campioni differiscano in qualche modo. Per esempio, hanno centri, spread o forme diverse. L’ipotesi alternativa è che i trattamenti abbiano effetti diversi.
Prepara i tuoi dati per il test.
Passo 1: Ordina i tuoi dati in blocchi (colonne in un foglio di calcolo).Per questo esempio, abbiamo 12 pazienti che ricevono tre trattamenti diversi.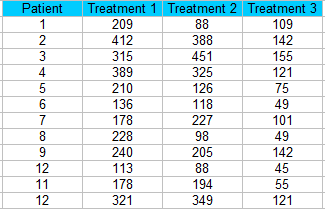
Passo 2: Classifica ogni colonna separatamente. Il punteggio più piccolo dovrebbe avere un rango di 1. Sto facendo la classifica per righe, quindi ogni paziente è classificato con 1, 2 o 3 per ogni trattamento.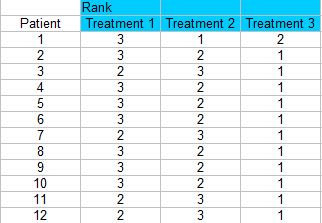
Passo 3: Somma i ranghi (trova un totale per ogni colonna).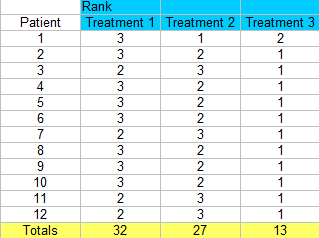
Esegui il test
Nota: Questo test di solito non viene eseguito a mano, poiché i calcoli richiedono molto tempo e lavoro. Quasi tutti i pacchetti software statistici più diffusi possono eseguire questo test. Tuttavia, sto includendo i passi manuali qui per riferimento.
Passo 4: Calcolare la statistica del test. Avrete bisogno di:
- n: il numero di soggetti (12)
- k: il numero di trattamenti (3)
- R: I ranghi totali per ciascuna delle tre colonne (32, 27, 13).
Inserite questi dati nella seguente formula e risolvete: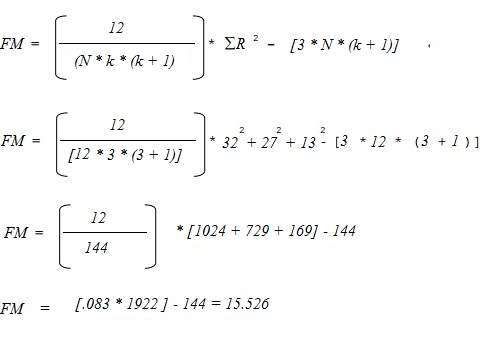
Passo 5: Trovate il valore critico FM dalla tabella dei valori critici di Friedman (vedi tabella sotto).
Utilizzate la tabella k=3 (perché è il numero di trattamenti che abbiamo) e un livello alfa del 5%. Potreste scegliere un livello alfa più alto o più basso, ma il 5% è abbastanza comune – quindi usate la tabella del 5% se non conoscete il vostro livello alfa.
Cercando n-12 in quella tabella, troviamo un valore critico FM di 6,17.
Passo 6: Confrontate la statistica del test FM calcolata (Passo 4) con il valore critico FM (Passo 5). Rifiutare l’ipotesi nulla se il valore F calcolato è più grande del valore critico FM.:
- Statistica di prova FM calcolata = 15,526.
- Valore critico FM dalla tabella = 6,17.
La statistica FM calcolata è più grande, quindi si rifiuta l’ipotesi nulla.
Tabella dei valori critici dell’ANOVA di Friedman per gradi
Tre tabelle secondo “k”.
Se il vostro k è superiore a 5, o il vostro n è superiore a 13, usate la tabella dei valori critici del chi quadrato al punto 5 per ottenere il valore critico.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6.00 | 9.39 |
| ∞ | 4.61 | 5.99 | 9.21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 |
Riferimento:
Analisi a due vie di Friedman della varianza per ranghi – Analisi dei dati k-contro-gruppo con una variabile di risposta quantitativa
. Recuperato il 7-17-2016 da: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. “Test di Friedman / Analisi della varianza a due vie per gradi” Da StatisticsHowTo.com: Statistica elementare per il resto di noi! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Hai bisogno di aiuto per un compito o un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!