Quando si tratta di carica elettrica e campo sappiamo quasi tutto su di esso, ma che dire della legge di Gauss? La legge di Gauss è un argomento importante in questo capitolo, ma prima di approfondire la legge di Gauss abbiamo bisogno di capire cos’è la superficie gaussiana e come determinare una superficie gaussiana?
Prima di procedere su come determinare una superficie gaussiana cerchiamo di capire cos’è una superficie gaussiana.

Cos’è una superficie gaussiana?

Superficie sulla quale l’angolo (ө) tra il campo elettrico (E) e il vettore area (A) è sempre costante in ogni punto, questo tipo di superficie è noto come superficie gaussiana.
Forse non hai capito il termine campo elettrico o vettore area. Quindi per conoscere il campo elettrico ho un articolo dedicato alla carica elettrica e al campo, quindi leggete pure.
Sappiamo che una quantità vettoriale ha magnitudine e direzione, quindi i vettori area sono vettori di superficie piana la cui magnitudine è l’area della superficie e la direzione è perpendicolare alla superficie.

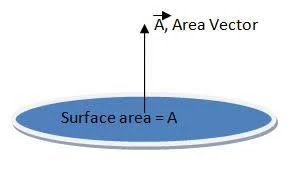
Vettore d’area

Ebbene, come si fa a identificare una superficie gaussiana se se ne vede una?

Come determinare una superficie gaussiana?

Sappiamo che la superficie gaussiana segue la legge di Gauss e l’angolo (ө) tra il campo elettrico (E) e il vettore area (A) è sempre uguale in ogni punto. Quindi per determinare una superficie gaussiana dobbiamo solo controllare se in ogni punto di una superficie l’angolo (ө) è lo stesso o no.
La legge di Gauss:

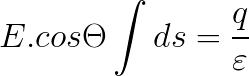
Ecco i passi per determinare una superficie gaussiana:
Passo 1: Selezionare la superficie da un corpo o un oggetto
Così spesso la gente si confonde e comincia a controllare se l’angolo è lo stesso per tutti i punti su un corpo o no. Bene, quello che deve essere chiaro è che vogliamo identificare se una superficie su un corpo è una superficie gaussiana o no e quindi controllare l’angolo (ө) in ogni punto della superficie e non in ogni punto dell’intero corpo.

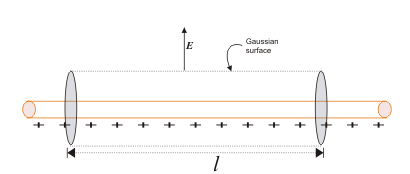
Identificare una superficie

Nell’immagine sopra stiamo considerando la regione non ombreggiata per trovare se è una superficie gaussiana o no e la regione ombreggiata non è considerata perché dobbiamo trovare se una superficie in un oggetto è una superficie gaussiana o no.
P.s: Significa che un corpo può avere più di 1 superficie gaussiana.
Passo 2: Controllare la direzione del campo elettrico (E)
Ora dopo aver deciso la superficie è necessario controllare la direzione del campo elettrico dalla superficie.
Da dove escono le linee del campo elettrico su una superficie.

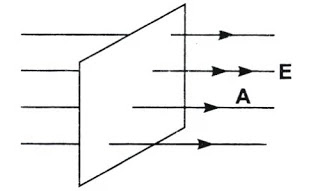
Direzione del campo elettrico

Se non conosci il campo elettrico o le linee di campo elettrico abbiamo un altro articolo su questo, leggi anche quello perché abbiamo fornito anche delle note scritte a mano con ogni derivazione del campo elettrico e della superficie e legge gaussiana. Clicca qui per leggere quell’articolo
Passo 3: Controllare il vettore area (A)
Dopo aver controllato la direzione del campo elettrico è necessario controllare il vettore area della superficie. Il vettore area è in realtà un vettore la cui direzione è sempre perpendicolare alla superficie.
Passo 4: Controllare l’angolo tra il vettore area (A) e il campo elettrico (E)
Dopo aver determinato la direzione del campo elettrico e del vettore area, è il momento di scoprire l’angolo (ө) tra di loro.

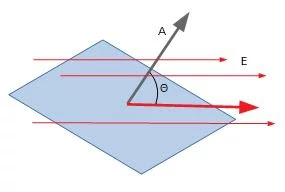
Angolo tra il vettore area e il campo elettrico

Controlla se l’angolo tra entrambi è uguale in tutti i punti. Se sì, allora è una superficie gaussiana.

Bene, una domanda che può avervi colpito è perché è necessario determinare una superficie gaussiana, perché è così importante?

Perché è necessario determinare una superficie gaussiana e come ci aiuta?

La superficie gaussiana ci aiuta nella valutazione del campo elettrico dovuto a diverse distribuzioni di carica. Clicca qui per andare all’articolo e scaricare gli appunti.

Alcuni esempi di superficie gaussiana:

Quindi alcuni esempi di superficie gaussiana sono:
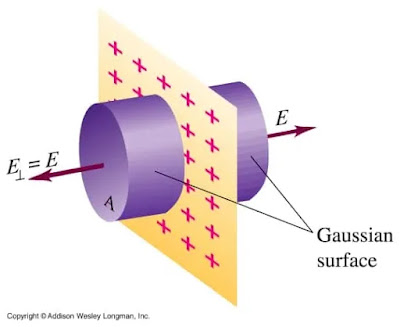
1. Superficie gaussiana cilindrica immaginaria creata per trovare il campo elettrico dovuto a un conduttore rettilineo carico. Troverete anche questa derivazione nei nostri appunti 🙂

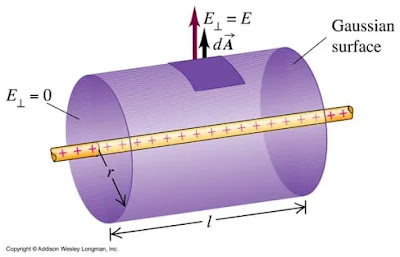
2. Superficie gaussiana cilindrica immaginaria creata per scoprire il campo elettrico dovuto a un foglio di carica piana. Troverete anche questa derivazione nei nostri appunti 🙂