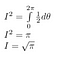Lord Kelvin ha scritto di questo integrale: “Un matematico è uno a cui ciò è ovvio come lo è per te che due volte due fa quattro.”
Godetevi 😉
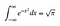
OK, quindi presumo che tu conosca un po’ di integrazione e differenziazione di base. Quanto segue aggiungerà un po’ di intuizione ai trucchi intelligenti che verranno dopo. Non preoccupatevi se alcune cose sono un po’ sconcertanti, cercate solo di capire cosa sta succedendo.
La strategia qui sarà quella di fare una sostituzione intelligente. Ma faremo una sostituzione in due variabili. Potete visualizzare il problema attuale come il calcolo dell’area sotto una curva
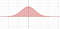
Ma mostreremo che il problema può essere trasformato nel calcolo di un volume.
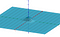
Per calcolare il volume, usiamo una formula di cambio di variabile leggermente diversa da quella usata nei normali integrali. Useremo le coordinate polari. Questo esprime le coordinate x e y in termini del loro raggio e del loro angolo. Geogebra ha un bel modo interattivo di vederlo qui

Poi useremo la formula magica del cambio di base per le coordinate polari.
Quando calcoliamo l’area sotto la curva, abbiamo l’elemento ‘dx’ che rappresenta una piccola distanza lungo l’asse x. Quando calcoliamo un volume, abbiamo dx dy, che è come un piccolo rettangolo con lato di lunghezza dx e dy. Usiamo poi queste basi per creare una serie di caselle che stimano il volume. Questo è più facile da vedere con la visualizzazione qui sotto. L’integrale è il limite di queste approssimazioni.
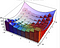
Quando, invece, usiamo il sistema di coordinate polari, abbiamo un elemento di area leggermente diverso sotto. Sotto, dA è l’elemento d’area. Con piccoli cambiamenti nell’angolo e nel raggio, questo elemento d’area può essere approssimato sempre meglio da un rettangolo con lato di lunghezza dr e r*dtheta rispettivamente. Se siete a vostro agio con un po’ di geometria, per piccoli theta sin(theta) è approssimato molto bene da theta e potete quindi dimostrare il risultato seguente.
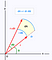
Risolvere l’integrale
Prima di tutto diamo un nome al nostro integrale. Lo chiamiamo I.
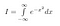
Nota che x è solo una ‘variabile fittizia’. L’area esiste indipendentemente dal nome della variabile che usiamo. Quindi, possiamo anche scrivere le seguenti due equazioni
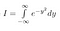
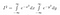
Ora, poiché I è solo una costante, sebbene non ne conosciamo ancora il valore, possiamo usare le nostre normali regole per portare una costante all’interno di un integrale
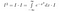
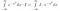
Finora non abbiamo fatto molto di concreto. Ora pensiamo bene al significato dell’integrale. Prendiamo integrali di funzioni. Se due funzioni prendono lo stesso valore ovunque, sono uguali e hanno la stessa area. Con questo in mente, possiamo fare le seguenti manipolazioni, se consideriamo I*exp(-x²) come una funzione di x, cioè qualcosa che prende valori di x come input, e dà un numero come output.
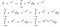
Ok, questo era molto da assimilare. Nella prima riga, abbiamo semplicemente riscritto I nella sua forma integrale con un nome di variabile diverso. Nella seconda riga, trattando I*exp(-x²) come una funzione, ci siamo resi conto che possiamo portare l’exp(-x²) all’interno dell’integrale dy, e questo darebbe ancora lo stesso valore di uscita per qualsiasi valore di x in ingresso. Infine, abbiamo usato le regole dell’esponenziazione.
Scrivendo il tutto, ora abbiamo
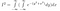
Poi arriva l’intuizione killer. Sopra abbiamo pasticciato con i nomi delle variabili e come rappresentare una funzione. Ora spostiamo la nostra prospettiva: questa espressione rappresenta anche l’integrale di exp(-(y²+x²)) su tutto il piano 2D, con elemento di area dA = dx dy. Cioè dx dy è un piccolo rettangolo su un piano, e exp(-(y²+x²)) è l’altezza sopra quel rettangolo.
Poi usiamo le intuizioni sulle coordinate polari di prima
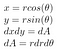
Come sin² + cos² = 1, dopo aver inserito tutto, otteniamo
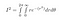
r va da 0 a infinito e theta va da 0 a 2*pi, perché questo copre tutto il piano 2D: qualsiasi punto ha un raggio minore di infinito, e un angolo tra 0 e 2pi radianti.
Possiamo valutare l’integrale interno usando la regola della catena
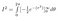
E, nella terra promessa ci troviamo ora: