Eventi casuali che hanno luogo in uno spazio campione continuo possono invocare immagini geometriche per almeno due ragioni: per la natura del problema o per la natura della soluzione.

Alcuni problemi, come l’ago di Buffon, gli uccelli sul filo, il paradosso di Bertrand, o il problema del bastone rotto in tre pezzi, per loro natura si presentano in un ambiente geometrico. Quest’ultimo ammette anche riformulazioni multiple che richiedono il confronto delle aree delle figure geometriche. In generale, possiamo pensare alle probabilità geometriche come a quantità non negative (non superiori a 1) che vengono assegnate a sottoregioni di un dato dominio in base a certe regole. Se la funzione μ è un’espressione di questa assegnazione definita su un dominio D, allora, per esempio, richiediamo

0 ≤ μ(A) ≤ 1, A ⊂ D e
μ(D) = 1

La funzione μ non è solitamente definita per tutti gli A ⊂ D. Quei sottoinsiemi di D per cui μ è definito sono gli eventi casuali che formano un particolare spazio campione. Molto spesso μ è definito per mezzo del rapporto delle aree così che, se σ(A) è definito come l'”area” dell’insieme A, allora si può impostare μ(A) = σ(A) / σ(D).

Problema 1

Due amici che prendono la metropolitana per andare al lavoro dalla stessa stazione arrivano alla stazione in modo uniforme e casuale tra le 7 e le 7:20 del mattino. Sono disposti ad aspettarsi a vicenda per 5 minuti, dopodiché prendono un treno insieme o da soli. Qual è la probabilità del loro incontro alla stazione?

In un sistema cartesiano di coordinate (s, t), un quadrato di lato 20 (minuti) rappresenta tutte le possibilità degli arrivi mattutini dei due amici alla stazione della metropolitana.

La zona grigia A è delimitata da due rette, t = s + 5 e t = s – 5, in modo che all’interno di A, |s – t| ≤ 5. Ne segue che i due amici si incontreranno solo se i loro arrivi s e t cadranno nella regione A. La probabilità che questo accada è data dal rapporto tra l’area di A e l’area del quadrato:

/ 400 = 175/400 = 7/16.

Problema 2

(.)

Tre punti A, B, C sono posti a caso su un cerchio di raggio 1. Qual è la probabilità che ΔABC sia acuto?

Fissiamo il punto C. Le posizioni dei punti A e B sono quindi definite da archi α e β che si estendono da C in due direzioni. A priori sappiamo che 0 < α + β < 2π. I valori favorevoli per il nostro problema di α e β (come angoli acuti sottesi soddisfano) 0 < α < π e 0 < β < π. La loro somma non può essere minore di π perché questo renderebbe l’angolo C ottuso, quindi, α + β > π. La situazione è presentata nel seguente diagramma dove il quadrato ha il lato 2π.

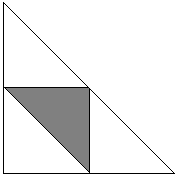
La regione D è l’intersezione di tre semipiani: 0 < α, 0 < β, e α + β < 2π. Questo è il grande triangolo nel diagramma sopra. Gli eventi favorevoli appartengono al triangolo ombreggiato che è l’intersezione dei semipiani α < π, β < π, e α + β > π. Il rapporto delle aree dei due è ovviamente 1/4.

Ora osservate che, a meno che il triangolo casuale sia acuto, può essere pensato come ottuso poiché la probabilità che due dei tre punti A, B, C formino un diametro è 0. (Perché BC sia un diametro, si dovrebbe avere α + β = π che è una linea retta, con zero come unica assegnazione possibile di area). Così possiamo dire che la probabilità che ΔABC sia ottuso è 3/4. Per un triangolo ottuso, il cerchio può essere diviso in due metà con il triangolo che giace interamente in una delle metà. Ne segue che 3/4 è la risposta alla seguente domanda:

Tre punti A, B, C sono posti a caso su un cerchio di raggio 1. Qual è la probabilità che tutti e tre si trovino in un semicerchio?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Probabilità geometriche

• Probabilità geometriche
• La maggior parte dei triangoli sono ottusi?
  • Otto selezioni in sei settori
  • Tre punti casuali su un cerchio
• Probabilità geometrica
  • Bastone rotto in tre pezzi (coordinate trilineari)
  • Bastone rotto in tre pezzi. Soluzione in coordinate cartesiane
• Paradosso di Bertrand
• Uccelli sul filo (problema e simulazione interattiva)
  • Uccelli sul filo: Soluzione di Nathan Bowler
  • Uccelli sul filo. Soluzione di Mark Huber
  • Birds on a Wire: una simulazione probabilistica. Soluzione di Moshe Eliner
  • Birds on a Wire. Soluzione di Stuart Anderson
  • Birds on a Wire. Soluzione di Bogdan Lataianu
• Simulazione della pasta di Buffon
• Fare la media delle gocce di pioggia – un esercizio di probabilità geometrica
  • Fare la media delle gocce di pioggia, parte 2
• Rettangolo su una scacchiera: un’introduzione
• Marcare e rompere i bastoni
• Punti casuali su un segmento
• Copertura del semicerchio
• Copertura della semisfera
• Intervalli casuali sovrapposti
• Intervalli casuali con una dominante
• Punti su una griglia quadrata
• Probabilità piane su una sfera
• Probabilità in un triangolo

|Contatto||Prima pagina||Contenuti||Up|

Copyright © 1996-2018 Alexander Bogomolny