Lo zero è un numero che cade esattamente tra i numeri positivi e negativi sulla linea dei numeri. Lo zero è considerato un numero intero, insieme ai numeri naturali positivi (1, 2, 3, 4…) e ai numeri negativi, (…-4,-3,-2,-1).

Lo zero è un numero speciale tra i numeri interi perché è l’unico intero che non è né positivo né negativo. È anche l’unico numero intero che non è né primo né composto. È considerato un numero pari perché è divisibile per 2 senza resto. Lo zero è l’elemento di identità additiva in vari sistemi di algebra, e la cifra “0” è usata come valore segnaposto nei sistemi di notazione posizionale per rappresentare i numeri.

Lo zero ha molte proprietà interessanti che lo rendono interessante per i matematici. Se si aggiunge o si sottrae lo zero da qualsiasi numero, il numero rimane lo stesso. Se si moltiplica 0 per qualsiasi numero, il risultato è 0. Qualsiasi numero elevato alla potenza zero è 1, quindi 20=1 e 560=1. Nell’algebra tradizionale, la divisione per 0 è indefinita, quindi nessun numero può essere diviso per 0. Il numero 0 è anche un elemento dei numeri reali e dei numeri complessi.

Storia del numero 0

Da dove viene l’idea dello zero? Al giorno d’oggi, ci sembra intuitivo; lo zero è un numero che sta per una quantità nulla, un niente. Vediamo gli zeri ovunque nella società, e capiamo naturalmente cosa significano e come possono essere manipolati matematicamente. Storicamente, però, il concetto di 0 ha impiegato un po’ di tempo per essere universalmente riconosciuto come un oggetto della matematica, e molti nel corso della storia hanno sostenuto che il numero zero non esiste, o che l’idea zero è un concetto incoerente.

Molte società antiche non avevano un concetto esplicito della quantità di zero o una cifra specifica da usare per la sua rappresentazione. Gli antichi egizi e i babilonesi avevano entrambi un’idea di una quantità nulla e una necessità di valori segnaposto nella rappresentazione dei numeri, ma non hanno mai sviluppato una cifra distinta o un concetto per rappresentare quella quantità o quel valore segnaposto. Gli antichi sistemi di numerazione egiziani erano interamente pittorici e non avevano valori posizionali, mentre gli antichi babilonesi usavano spazi tra i numeri per rappresentare valori posizionali.

I Maya avevano un concetto esplicito di 0 e avevano una cifra distinta per rappresentare il concetto e usarlo come valore segnaposto nel loro sistema di calendario vigesimale (base 20). Mentre i Maya, gli Olmechi e altre società precolombiane furono tra le prime nella storia ad avere una comprensione esplicita e sofisticata del numero 0, questi sistemi non hanno influenzato le società del Vecchio Mondo in Europa.

Gli antichi greci, d’altra parte, avevano una relazione complicata con lo zero. Non avevano un simbolo per il suo concetto o per il suo valore segnaposto perché non erano sicuri che il numero 0 potesse essere considerato una cosa realmente esistente. Come, si chiedevano, poteva qualcosa (un numero) essere niente (zero)? Per i greci, i numeri naturali (1, 2, 3, 4,…) erano derivati dalla nostra comprensione di oggetti individuali discreti nel mondo. Aristotele stesso ha notoriamente sostenuto che lo 0 non esiste, sulla base del fatto che lo 0 rappresenta il vuoto o il nulla, e un vero vuoto o il nulla non può esistere.

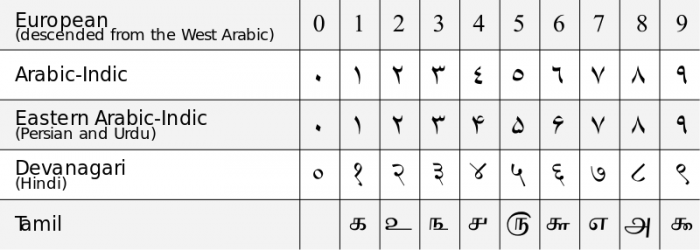
I cinesi avevano una comprensione dello “0” come cifra segnaposto per i loro sistemi di conteggio, ma non consideravano la cifra “0” come un numero distinto, solo un simbolo utile. La comprensione comune dello 0 come numero distinto e come cifra per i sistemi di notazione posizionale venne dall’India durante il VI secolo d.C. I matematici indiani dell’epoca svilupparono i primi tipi di sistemi di notazione decimale (base 10) che incorporavano lo 0 come cifra distinta e avevano una comprensione delle proprietà matematiche uniche dello zero. Nell’XI secolo d.C., l’idea dello zero si era diffusa in Europa occidentale attraverso l’influenza dei matematici islamici che vivevano in Spagna sotto il califfato degli Omayyadi, e fu creato l’odierno sistema numerico arabo di notazione decimale. Il primo uso della parola inglese “zero” risale al 1589.

Proprietà matematiche dello zero

Il numero zero gioca un ruolo integrale in quasi ogni campo della matematica. Lo zero è il più piccolo numero intero non negativo e non ha nessun numero naturale che lo precede. Poiché lo 0 è un numero intero, è anche un numero razionale, un numero reale e un numero complesso. In matematica, lo 0 è considerato una quantità che corrisponde a una quantità nulla. Si potrebbe dire che lo zero è la “quantità” posseduta da un insieme che non ha membri.

In algebra

In algebra elementare, lo zero è spesso espresso come se si trovasse al centro della linea dei numeri. Il numero 0 è considerato un numero pari in quanto è un multiplo intero del numero 2 (2×0=0). Lo 0 non è un numero primo perché ha una quantità infinita di fattori, e non è un numero composto perché nessun prodotto di due numeri primi è uguale al numero 0.

Per quanto riguarda i 4 operatori aritmetici principali (+, -, ×, ÷) e l’operazione esponente, il numero 0 si comporta secondo le seguenti regole:

• Addizione: x+0=0+x=x. Lo zero è considerato l’elemento identitario additivo in quanto qualsiasi numero più o meno zero è uguale a quel numero
• Sottrazione: x-0=x e 0-x=-x
• Moltiplicazione: x⋅0=0⋅x=0. Qualsiasi numero per 0 è anche uguale a 0.
• Divisione: 0/x=0, tranne quando x=0. x/0 è una quantità matematicamente indefinita, poiché 0 non ha un inverso moltiplicativo (nessun numero per 0 dà 1).
• Esponenti: x0=1, tranne quando x=0. C’è stato un lungo dibattito sul fatto che 00 sia indefinito o un’espressione ben formata. Per tutte le x positive, 0x=0.

In espressioni che coinvolgono i limiti, la quantità 0/0 può comparire nel contesto della dimostrazione dei limiti di funzioni razionali come f(x)/g(x). In questi casi, 0/0 non è indefinito ma rappresenta una forma indeterminata. Questo non significa che il limite è indefinito ma che deve essere calcolato con un altro metodo, come trovare le derivate. Esistono alcuni modelli algebrici in cui la divisione per zero dà una quantità definita, come la linea reale proiettivamente estesa o la sfera di Riemann.

Nella teoria degli insiemi

Nella teoria degli insiemi, il numero 0 corrisponde alla cardinalità dell'”insieme vuoto” o “insieme nullo” (comunemente rappresentato come {} o {∅}. La cardinalità di un insieme è la quantità di elementi in quell’insieme, se non si hanno arance, allora si ha un insieme di 0 arance (un insieme vuoto di arance).

Lo zero è spesso usato come punto di partenza nella teoria degli insiemi per costruire il resto dei numeri naturali. Queste costruzioni di von Neumman, dal nome del famoso polimatico John von Neumann, costruiscono i numeri naturali definendo 0={} e definiscono una funzione successore S(a) = a ∪ {a}. L’insieme dei numeri naturali può essere costruito dalle applicazioni ricorsive della funzione successore a partire dall’insieme vuoto:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}, {{}}}}

e così via. Seguendo questo schema, si può costruire l’intero insieme infinito dei numeri naturali. In questo modo, possiamo dire che ad ogni numero naturale corrisponde l’insieme che contiene tutti i numeri naturali che lo precedono.

In fisica

Nel contesto delle misurazioni quantitative in fisica, 0 è considerato la linea di base da cui vengono fatte tutte le altre misurazioni di unità. Molto spesso, la linea di base di 0 corrisponde a qualche variabile fisicamente significativa che è naturalmente distinguibile da tutte le altre grandezze di misura.

Per esempio, nella scala Kelvin, una temperatura di 0 K corrisponde allo 0 assoluto – la temperatura più fredda che è fisicamente possibile. Nella scala di temperatura Celsius, 0 °C è definito come il punto di congelamento dell’acqua alla pressione atmosferica. Nel contesto della dinamica e dell’elettromagnetismo, un valore di 0 è dato alla posizione in cui un sistema ha la minima quantità possibile di energia potenziale. Per esempio, allo stato fondamentale di un atomo, il livello di energia più basso possibile per gli elettroni dell’atomo, viene spesso assegnato il valore 0.

Analogamente, nel contesto della cinematica, il quadro di riferimento da cui vengono fatte le osservazioni del moto è definito come avente un punto centrale che giace sull’origine dell’asse delle coordinate nel punto (0, 0). Nel caso di quantità conservate, come massa-energia, quantità di moto e momento angolare, la quantità totale di cambiamento delle quantità conservate in un sistema isolato è sempre uguale a 0.

In informatica

I computer immagazzinano informazioni sotto forma di sequenze di 1 e 0 lunghe come bit. In questa rappresentazione binaria, lo 0 corrisponde a una posizione “off” e si contrappone alla posizione “on” designata da 1. Un valore di 0 su un circuito elettrico significa che il circuito è spento e non ha alcun flusso elettrico. Allo stesso modo, molte logiche computazionali definiscono “0” come il carattere che rappresenta un falso valore di verità.

Nei database dei computer, gli elementi di una matrice sono contati usando un sistema di conteggio basato su zero. Ciò significa che per un insieme con n elementi, gli elementi hanno indici che iniziano con 0. Così, un elemento con un numero di indice di 0 è effettivamente il primo elemento della serie, e un numero di indice di 1 corrisponde al secondo elemento, e così via. In generale, l’ennesimo termine di un insieme ha un numero di indice corrispondente a n-1. Questo sistema di conteggio può causare confusione ai nuovi programmatori che sono abituati ad assegnare intuitivamente valori di indice che iniziano con 1.

.