Il modello Ising è un particolare esempio di sistema termodinamico, ed è il sistema modello per comprendere le transizioni di fase. Sapete come molti biologi passano tanto tempo con dei miseri moscerini della frutta? Bene, i fisici passano un sacco di tempo con il modello di Ising. Come ci dice il Prof. Raghu, è la Drosophila delle transizioni di fase.

Personalmente, non sono il più grande fan della sua analogia perché penso che i moscerini della frutta siano disgustosi. Speriamo che il modello di Ising non sia troppo disgustoso.

Motivazione

Perché dovremmo passare così tanto tempo a parlare del modello di Ising?

• È sorprendentemente utile per aiutarci a pensare a tutti i tipi di comportamenti relativi alle transizioni di fase. Per esempio:

  • il modello di Ising mostra la rottura della simmetria nella fase a bassa temperatura (di cui abbiamo appena parlato)

  • ha uno speciale ‘punto critico’ ad una temperatura ben definita (a cui abbiamo accennato nel diagramma di fase dell’acqua)

  • altre ricche caratteristiche.

• È uno dei pochi modelli esattamente risolvibili in cui possiamo effettivamente calcolare le quantità termodinamiche e interpretarle.

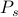  • In generale, calcolare le quantità termodinamiche è difficile perché bisogna sommare molti termini. Ricordate dalla nostra prima lezione di termodinamica che potete pensare a un sistema all’equilibrio come a un insieme di molti stati , ognuno pesato con la propria probabilità . In questo quadro, le quantità termodinamiche che si osservano corrispondono a medie sull’insieme. In particolare, se volete trovare la media dell’insieme di qualche osservabile 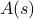, dovete trovare la somma 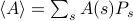, dove la somma corre su tutti gli stati possibili. Il problema con questo, come ricorderete, è che il numero di stati di un sistema termodinamico scala esponenzialmente con il numero di particelle! Anche per un sistema di dimensioni moderate, ci sono troppi stati perché un computer possa calcolare esplicitamente la media – per non parlare di un sistema termodinamico dove 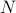è dell’ordine di .

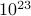  • Perciò dobbiamo ”essere intelligenti” per calcolare la funzione di partizione, e dovremmo essere grati per i sistemi esattamente risolvibili!

• Il modello di Ising è semplice, eppure può essere applicato a un numero sorprendente di sistemi diversi.

  • Questo è il nostro primo assaggio di universalità – una caratteristica dei fenomeni critici in cui la stessa teoria si applica a tutti i tipi di transizioni di fase diverse, sia nei liquidi che nei gas o nei magneti o nei superconduttori o altro. I fisici amano questo tipo di comportamento generale perché suggerisce una sorta di ordine più profondo nel nostro mondo caotico.

Definizione del Modello di Ising

Il Modello di Ising è un modello matematico che non corrisponde a un sistema fisico reale. È un enorme reticolo (quadrato) di siti, dove ogni sito può essere in uno dei due stati. Etichettiamo ogni sito con un indice , e chiamiamo i due stati e . Per dire che il sito è nello stato , scriviamo .

Ora, questa definizione è tristemente astratta e non fisica, quindi per noi fisici, è estremamente utile avere in mente un sistema reale, in modo da poter fare riferimento a qualcosa di esplicito e costruire l’intuizione fisica. Ecco alcuni sistemi fisici che il modello di Ising potrebbe rappresentare:

• Un magnete. Ogni sito rappresenta un particolare ‘spin’ nel materiale (un elettrone spaiato??), ed è se lo spin punta in basso o se lo spin punta in alto. Ognuno degli spin si comporta come un mini magnete con il suo mini momento magnetico; se tutti gli spin sono allineati, allora l’intero reticolo di spin si comporta come un grande magnete con un momento magnetico netto macroscopico.

• Una lega; diciamo, l’ottone. Ognuno dei siti è un atomo nel reticolo; rappresenta un atomo di rame in quel sito; rappresenta lo zinco.

• Un ”gas di reticolo”. Ognuno dei siti è la possibile ubicazione di una particella; significa che quel sito è vuoto e significa che quel sito è occupato da una particella.

• Lattiche di vortici batterici???

Per ora, penseremo al modello di Ising come a un modello di magnete. È un modello grossolanamente semplificato e giocattolo di un magnete, di sicuro, ma l’analogia del magnete può comunque aiutare a guidare la nostra cara intuizione fisica.

Mettere insieme l’hamiltoniana

Una domanda naturale da fare su questo modello di magnete a forma di topolino è quale energia ha. Per essere più precisi, vogliamo scrivere una funzione che rappresenta l’energia di ogni singola configurazione possibile (un microstato) degli spin nel magnete. Come sappiamo, questa funzione energetica si chiama Hamiltoniana.

Nel modello di Ising, l’Hamiltoniana include due tipi di interazioni:

• il termine di campo esterno. Come ricordiamo dalla meccanica quantistica, un campo magnetico esterno può dividere le energie degli stati di spin-down e spin-up, in modo che uno sia più alto in energia e l’altro sia più basso.

  • La dimensione di rappresenta quanto è forte il campo, quindi ci dice quanto è più alto in energia uno spin rispetto all’altro.

  • Il segno di ci dice se è preferito lo spin up o lo spin down.

  • Siccome ogni singolo spin sente il campo esterno, dobbiamo sommare tutti i siti per trovare il contributo totale all’energia.

• il termine di interazione tra spin vicini – forse vogliono allinearsi tra loro e puntare nella stessa direzione, forse vogliono anti-allinearsi e puntare in modi diversi. Fisicamente, possiamo immaginare che questa interazione nasce perché ogni spin nel magnete è il suo mini dipolo magnetico che stabilisce il suo campo magnetico, e i suoi vicini possono sentire quel campo magnetico.

  • La dimensione di ti dice quanto fortemente gli spin vicini sono accoppiati tra loro – quanto vogliono (anti-)allinearsi. Fisicamente, la forza dell’accoppiamento spin-spin potrebbe dipendere dalla distanza tra di loro nel reticolo del maget, per esempio.

  • Il segno di ti dice se i vicini preferiscono allinearsi o anti-allinearsi. (Il termine tecnico per questo è ferromagnetico o antiferromagnetico, rispettivamente). Fisicamente, se un materiale è l’uno o l’altro (o nessuno dei due) dipende dagli esatti dettagli di meccanica quantistica di come gli spin interagiscono.

  • Siccome l’interazione spin-spin nasce tra due spin, dobbiamo sommare su coppie di siti per trovare la sua interazione totale all’energia.

Più sul termine di interazione

Una domanda naturale sul termine di interazione spin-spin è quali spin sono accoppiati a quali spin?

Se torniamo di nuovo all’immagine fisica del magnete, e zoomiamo su qualche spin particolare, ci aspettiamo che la forza dell’interazione spin-spin sia più forte per gli spin vicini e più debole per quelli lontani. L’esatta dipendenza dalla distanza delle interazioni spin-spin è probabilmente piuttosto complicata per i magneti reali.

Per il modello di Ising, facciamo l’ipotesi più semplice possibile per la natura di questa interazione spin-spin:

Alcuni commenti:

• In un reticolo quadrato di dimensioni, ogni sito ha 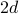vicini più vicini: sinistra e destra in una dimensione, su e giù quando si aggiunge la seconda dimensione, ecc.

• Parliamo spesso delle interazioni vicino-vicino come l’energia di un legame che unisce due siti del reticolo.

• Quando sommiamo su coppie di siti adiacenti, simbolicamente, scriviamo piccole parentesi angolari intorno agli indici per rappresentare il “vicino più vicino”.

Una bella conseguenza delle interazioni di vicinato è che quando troviamo l’energia totale di qualche configurazione di spin, piuttosto che sommare su tutte le possibili coppie di siti, sommiamo solo sulle coppie di siti che sono adiacenti tra loro.

Ora che abbiamo discusso tutte queste cose, siamo pronti a scrivere l’espressione effettiva dell’Hamiltoniana. (Ho voluto spiegare e interpretare la fisica prima di scrivere l’Hamiltoniana, in modo che i simboli avessero un senso.)

Hamiltoniana del modello di Ising

L’Hamiltoniana del modello di Ising può essere scritta come

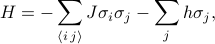
dove rappresenta l’interazione spin-spin, rappresenta il campo esterno, e gli 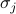sono gli spin individuali su ciascuno dei siti del reticolo. La prima somma è su tutte le coppie di siti di reticolo vicini (cioè i legami); rappresenta le interazioni tra le spine. La seconda somma è su tutti i siti del reticolo stesso; rappresenta il campo esterno che cerca di allineare tutte le spine in una direzione.

Continua con la termodinamica del modello Ising.