di Marco Taboga, PhD
La funzione indicatore di un evento è una variabile casuale che assume valore 1 quando l’evento accade e valore 0 quando l’evento non accade. Le funzioni indicatrici sono spesso usate nella teoria della probabilità per semplificare la notazione e dimostrare teoremi.
Definizione
Quella che segue è una definizione formale.
Definizione Sia 
uno spazio campione e un evento. La funzione indicatrice (o variabile casuale indicatrice) dell’evento , indicata con , è una variabile casuale definita come segue: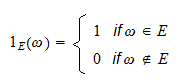
Mentre l’indicatore di un evento è solitamente indicato con , a volte è indicato anche condove è la lettera greca Chi.
Esempio Lanciamo un dado e uno dei sei numeri da 1 a 6 può apparire a faccia in su. Lo spazio campione èDefinire l’evento descritto dalla frase “Un numero pari appare a faccia in su”. Una variabile casuale che assume valore 1 quando un numero pari appare a faccia in su e valore 0 altrimenti è un indicatore dell’evento . La definizione caso per caso di questo indicatore è
Dalla definizione precedente, si può facilmente vedere che è una variabile casuale discreta con supporto e funzione di massa di probabilità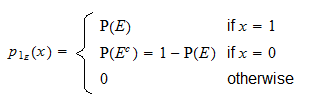
Proprietà
Le funzioni indicatore godono delle seguenti proprietà.
Potenze
La terza potenza di è uguale a :perché può essere o o e
Valore atteso
Il valore atteso di è uguale a :
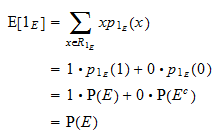
Varianza
La varianza di è uguale a . Grazie alla solita formula della varianza e alla proprietà delle potenze di cui sopra, otteniamo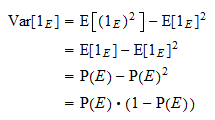
Intersezioni
Se e sono due eventi, alloraperché:
-
se
, allora e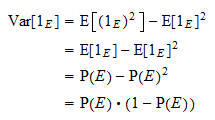
-
se
, allorae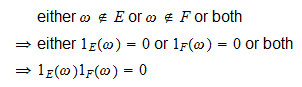
Indicatori di eventi a probabilità zero
Sia un evento a probabilità zero e una variabile casuale integrabile. Allora,Mentre una prova rigorosa di questo fatto è al di là dello scopo di questa esposizione introduttiva, questa proprietà dovrebbe essere intuitiva. La variabile casuale è uguale a zero per tutti i punti del campione tranne forse per i punti . Il valore atteso è una media ponderata dei valori che può assumere , dove ogni valore è ponderato dalla sua rispettiva probabilità. I valori non nulli che può assumere sono ponderati da probabilità zero, quindi deve essere zero.
Esercizi risolti
Qui sotto puoi trovare alcuni esercizi con soluzioni spiegate.
Esercizio 1
Consideriamo una variabile casuale e un’altra variabile casuale definita come una funzione di .
Esprimere usando le funzioni indicatore degli eventi e .
Denotiamo con l’indicatore dell’evento e denotiamo con l’indicatore dell’evento . Possiamo scrivere come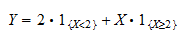
Esercizio 2
Sia una variabile casuale positiva, cioè una variabile casuale che può assumere solo valori positivi. Sia una costante. Dimostrare che dove è l’indicatore dell’evento .
Prima si noti che la somma degli indicatori e è sempre uguale a :Di conseguenza, possiamo scrivere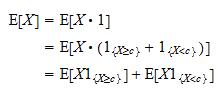
Ora, si noti che è una variabile casuale positiva e che il valore atteso di una variabile casuale positiva è positivo:Quindi,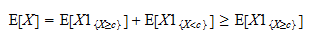
Esercizio 3
Sia un evento e denotiamo la sua funzione indicatore con . Sia il complemento di e denotiamo la sua funzione indicatore con . Puoi esprimere come funzione di ?
La somma dei due indicatori è sempre uguale a :Quindi,
Come citare
Per favore citare come:
Taboga, Marco (2017). “Funzioni indicatrici”, Lezioni di teoria della probabilità e statistica matematica, Terza edizione. Kindle Direct Publishing. Appendice online. https://www.statlect.com/fundamentals-of-probability/indicator-functions.