- Cos’è la forma dell’intercetta della pendenza
- Cos’è b in y=mx+b?
- Cos’è m in forma di intercetta di pendenza?
- Come scrivere un’equazione in forma di intercetta di pendenza?
- Come trovare l’intercetta y?
- Come trovare la pendenza di un’equazione?
- Cos’è una pendenza indefinita?
- Ricercare l’equazione da un punto
- Trovare la pendenza da due punti
- Equazione di una retta dati due punti
- Come trovare dominio e intervallo?
Cos’è la forma dell’intercetta della pendenza
La forma dell’intercetta della pendenza è una delle tre forme che possiamo usare per esprimere una linea retta. Le altre forme sono chiamate forma della pendenza del punto e forma standard, ma in questa sezione useremo principalmente la forma dell’intercetta della pendenza. Usando la forma pendenza-intercetta, esprimiamo l’equazione di una retta che è:
Potresti sapere che xxx e yyy sono coordinate di un punto su un grafico, ma cosa sono mmm e bbb?
Cos’è b in y=mx+b?
La lettera b è un numero che rappresenta quando la linea tocca l’asse y. Ci riferiamo anche a questo come “intercetta y”. Per esempio, disegniamo una linea retta sul piano delle coordinate.
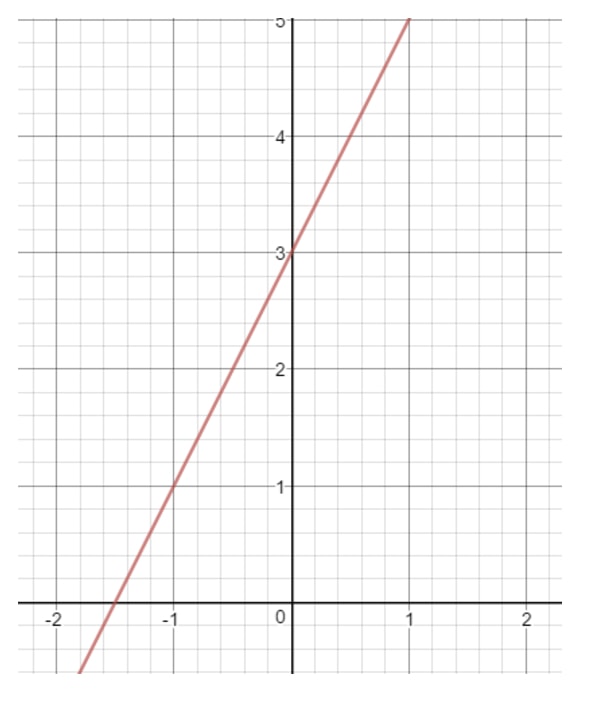
Se guardate attentamente l’asse y, la linea retta tocca l’asse y in un punto specifico. Dov’è questo punto? Sarebbe il numero 3, perché è lì che l’asse y e la linea si intersecano. Questo significa che possiamo concludere che b = 3.
Cos’è m in forma di intercetta di pendenza?
La lettera m è un numero che rappresenta la pendenza della linea. Alcune persone si riferiscono alla pendenza come salita su corsa. Ricordiamo che se abbiamo due punti, allora siamo in grado di trovare la pendenza dei due punti usando la formula della pendenza
La stessa idea funziona qui. Se prendiamo due punti qualsiasi su una linea retta, allora possiamo trovare la pendenza della linea usando la formula di cui sopra! Per esempio, usiamo questa linea.
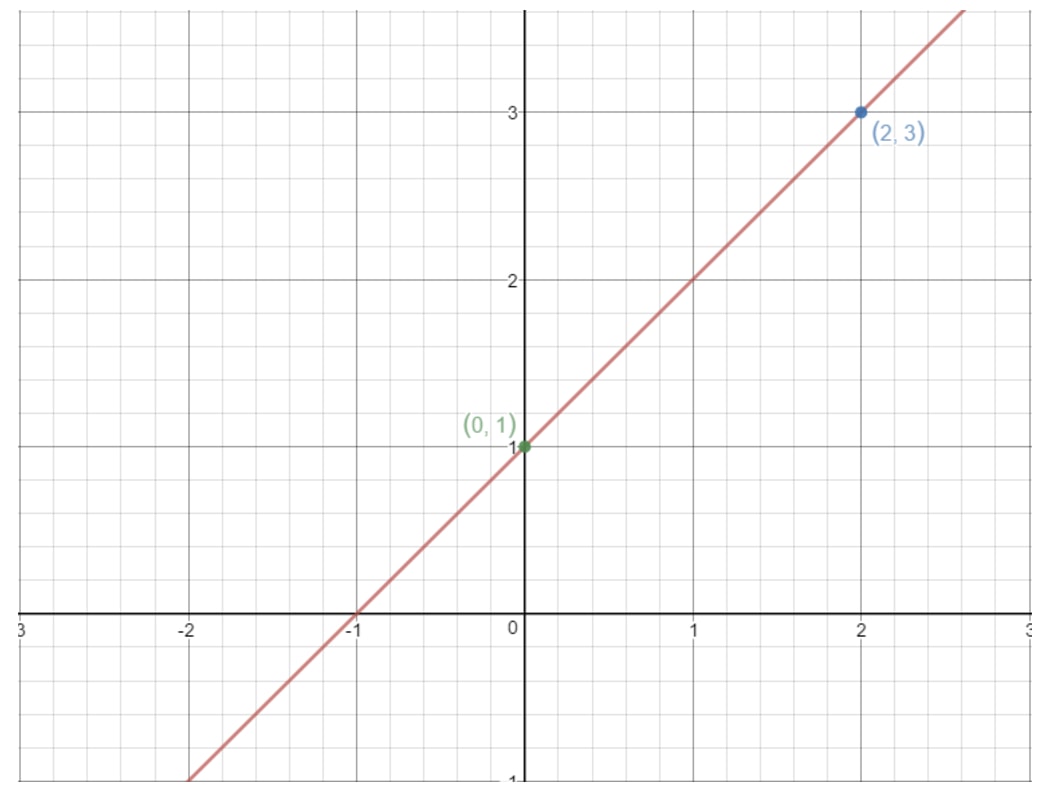
Nota che i punti (2, 3) e (0, 1) sono su questo grafico. Allora perché non usiamo questi due punti per trovare la pendenza della linea? Usando la formula, otterremmo:
Questo significa che la pendenza di questa linea è 111!
La cosa speciale delle pendenze è che possiamo usare qualsiasi due punti sulla linea per trovarla. Quindi, se prendete due punti diversi su questa linea, otterrete comunque che la pendenza è 111.
Come scrivere un’equazione in forma di intercetta di pendenza?
Potreste sapere com’è la forma di intercetta di pendenza, ma la metà delle volte vi verranno date equazioni che non sono in quella forma. Quindi il tuo compito è di trasformarle in forma di intercetta della pendenza. Come lo facciamo? L’obiettivo è quello di isolare sempre il termine yyy. Per esempio, diciamo che vi è data l’equazione
Per isolare yyy, spostiamo il 6x+46x + 46x+4 sul lato destro dell’equazione
Ora il 222 è in mezzo a yyy, quindi ce ne liberiamo dividendo entrambi i lati dell’equazione per 222.
Siccome yyy è isolata, si può vedere che è in forma di intercetta di pendenza y=mx+by = mx + by=mx+b dove m=-3m = -3m=-3, e b=-2b = -2b=-2.
Ora che conosciamo bene l’intercetta y e la pendenza, perché non guardiamo le domande specifiche per trovarle!
Come trovare l’intercetta y?
Domanda 1: Usando l’equazione lineare y=12x+5y = \frac{1}{2} x + 5y=21x+5, trovare l’intercetta y.
Nota qui che l’equazione è già nella forma intercetta della pendenza y=mx+by = mx + by=mx+b. Abbiamo solo bisogno di scoprire qual è bbb. Possiamo vedere che b=5b = 5b=5, quindi l’intercetta y è 555.
Facciamo una domanda un po’ più difficile.
Questione 2: Determinare l’intercetta y di 2x-4y=82x – 4y = 82x-4y=8
Ora questa equazione lineare non è in forma di intercetta di pendenza, quindi dobbiamo prima cambiarla in quella forma. Il nostro obiettivo è di isolare yyy in questa equazione.
Vedi che se spostiamo il 2x2x2x sul lato destro dell’equazione, avremo:
Ora dividendo entrambi i lati per -4-4-4, avremo:
Ora scambiando le posizioni dei due termini si ottiene:
Questione 3: Determinare l’intercetta y di 4y-8=04y – 8 = 04y-8=0.
Questo può sembrare un po’ strano perché non c’è il termine xxx, ma il nostro obiettivo rimane lo stesso. Stiamo per isolare yyy.
Spostare il -8-8-8 sul lato destro dell’equazione ci dà:
Dividendo entrambi i lati dell’equazione per 444 ci dà
Ora questo può non sembrare, ma l’equazione è in forma di intercetta di pendenza. È solo che m=0m = 0m=0, quindi l’intero termine mxmxmx è scomparso. Basta riscrivere l’equazione come
Dall’osservazione, si può dire che b=2b = 2b=2, e quindi l’intercetta y è 222. Facciamo un’altra domanda.
Questione 4: Determinare (se possibile) l’intercetta y di 5x-15=05x – 15 = 05x-15=0.
Questa è interessante perché l’equazione non ha il termine yyy. Quindi come possiamo metterla in forma di intercetta della pendenza? Beh, l’unica cosa che possiamo fare ora è isolare per xxx, quindi proviamo questo per ora.
Spostando il 151515 sul lato destro dell’equazione abbiamo:
Dividendo entrambi i lati dell’equazione si ottiene:
Ora disegneremo questo su un grafico. Notate che in questa equazione, xxx è costretto ad essere 333 e non può essere altro. Tuttavia, non dice nulla di yyy, quindi yyy può essere qualsiasi cosa voglia. Se dovessimo scrivere una tabella di valori, otteniamo:
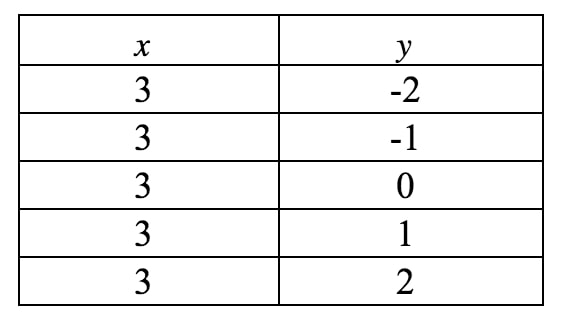
Se tracciamo questi punti su un piano di coordinate e disegniamo la retta, abbiamo:
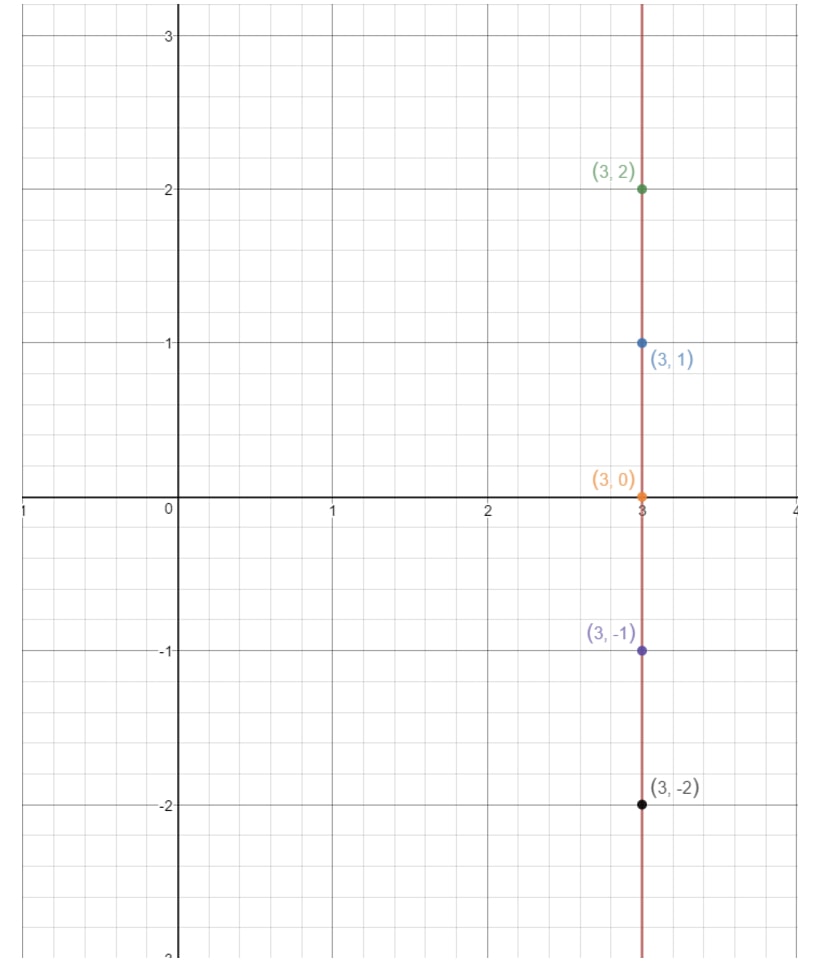
Nota come la linea non tocca mai l’asse y. Questo significa che l’equazione non ha un’intercetta y. Ora che abbiamo coperto tutti i casi di trovare l’intercetta y, guardiamo le domande che ci chiedono di trovare la pendenza!
Come trovare la pendenza di un’equazione?
Domanda 5: Trovare la pendenza di y=32x+1y = \frac{3}{2}x + 1y=23x+1
Domanda 6: Determinare la pendenza dell’equazione lineare 6x-6y=06x – 6y = 06x-6y=0
Come potete vedere, l’equazione non è in forma di intercetta di pendenza, quindi dobbiamo prima convertirla in questa forma. Il nostro obiettivo è quello di isolare yyy.
Spostare 6x6x6x sul lato destro dell’equazione dà:
Dividendo entrambi i lati per -6-6-6 dà:
Nota che questo è in realtà in forma di intercetta di pendenza y=mx+by = mx + by=mx+b. È solo che l’intercetta y bbb in questo caso è 000, e xxx è uguale a 1x1x1x. Quindi possiamo riscrivere l’equazione in:
Ora osservando, vediamo che m=1m = 1m=1. Poiché mmm è la pendenza, allora la pendenza deve essere 111. Facciamone una un po’ più difficile
Domanda 7: Determinare la pendenza di 2y-4=02y – 4 = 02y-4=0
Anche questa è un po’ strana perché non abbiamo un termine xxx. Tuttavia, il nostro obiettivo di isolare yyy rimane lo stesso.
Spostando -4-4-4 sul lato destro dell’equazione abbiamo:
Dividendo entrambi i lati dell’equazione per 222 si ottiene:
Vedi qui che ora è in forma di intercetta di pendenza, tranne il termine mxmxmx è nascosto perché m=0m = 0m=0. Quindi possiamo riscrivere la nostra equazione come:
Siccome m=0m = 0m=0, allora abbiamo una pendenza zero. Se ti stai chiedendo come appare una linea con pendenza 000, eccoti un grafico da vedere.
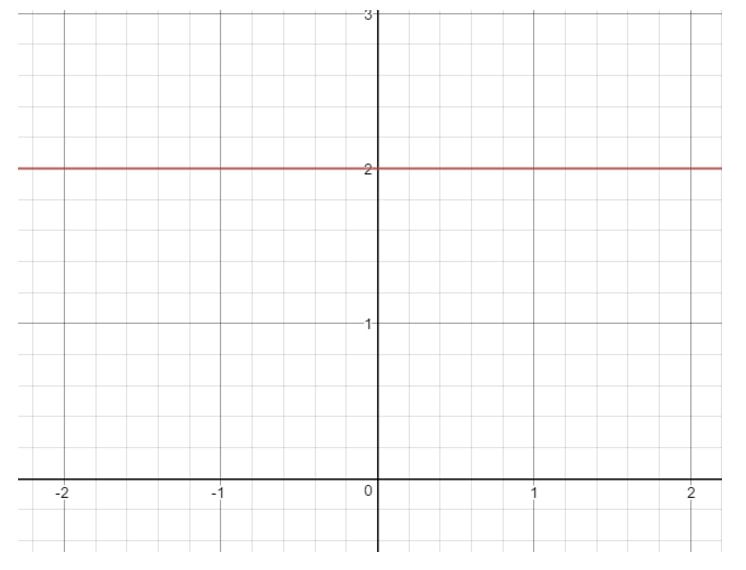
Questione 8: Trova (se possibile) la pendenza dell’equazione lineare 16-4x=016 – 4x = 016-4x=0
In questo caso, yyy non può essere isolata perché non c’è il termine yyy. Quindi l’unica cosa che possiamo fare è isolare xxx.
Spostare 161616 sul lato destro dell’equazione dà:
Dividendo entrambi i lati per -4-4-4, si ottiene:
Questo non è ancora in forma di intercetta di pendenza, quindi la nostra unica speranza di ottenere la pendenza è di disegnare un grafico di questa linea. Di nuovo, vediamo che xxx è sempre costretto ad essere 444, ma yyy può essere qualsiasi cosa voglia perché non c’è un termine yyy. Se dovessimo scrivere una tabella di valori, otteniamo:
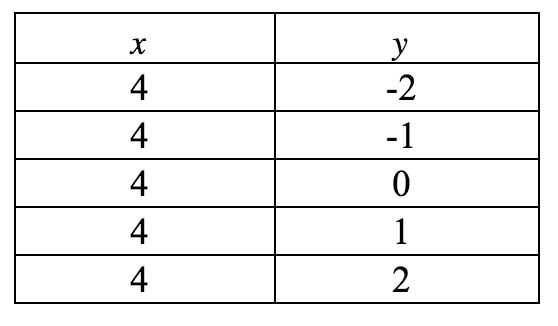
Se tracciamo questi punti su un piano di coordinate e disegniamo la retta, abbiamo:
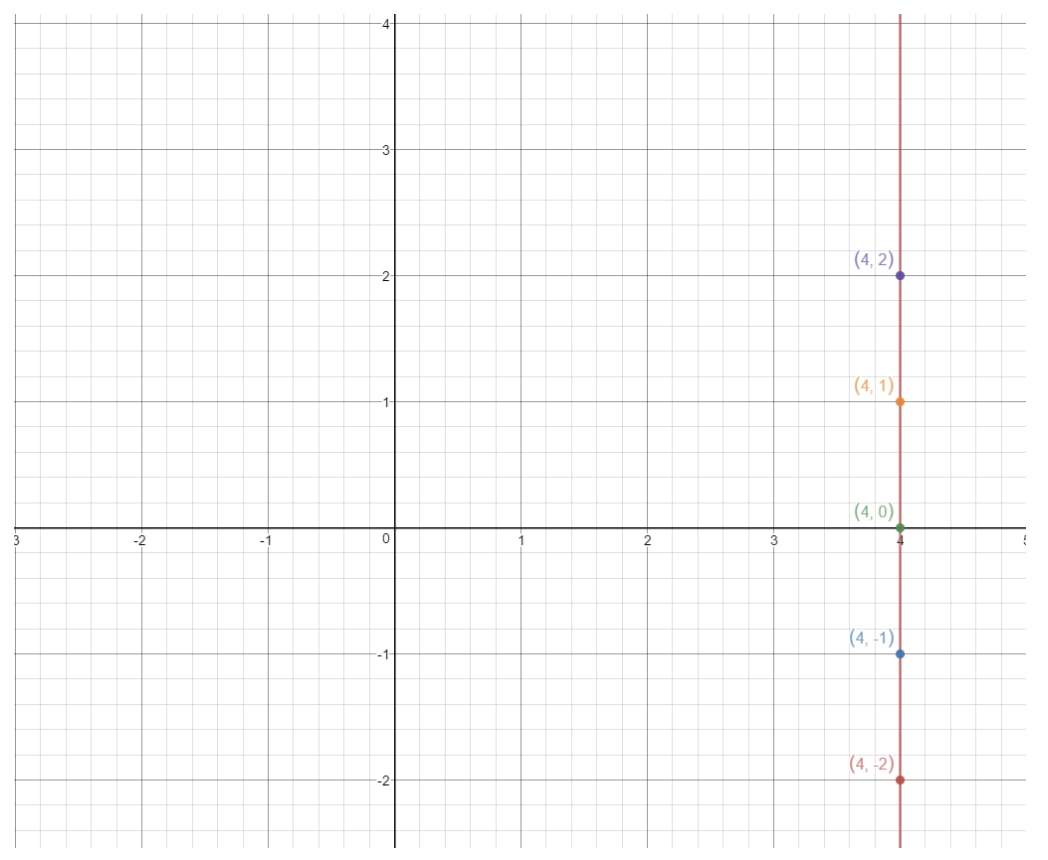
Questa è una linea verticale. Qual è la pendenza di una linea verticale? Cerchiamo di capirlo trovando la salita e la discesa. Vedete come questa linea sale sempre all’infinito, ma non c’è nessun tipo di pendenza. Questo significa che la pendenza è 000. Quindi se calcoliamo la pendenza, allora otterremo:
Non possiamo dividere per 000, quindi abbiamo effettivamente una pendenza indefinita.
Cos’è una pendenza indefinita?
Una pendenza indefinita è una pendenza che va dritta nel grafico. Come si vede nel grafico qui sopra, la pendenza sale all’infinito e non ha una corsa. Di conseguenza, otteniamo una pendenza indefinita perché non possiamo dividere per 000.
In generale, otteniamo sempre una pendenza indefinita ogni volta che otteniamo una linea verticale dritta!
Guardiamo alcune altre domande uniche!
Ricercare l’equazione da un punto
Questione 9: Un punto (2, 6) passa per un’equazione di y=-5x+by = -5x + by=-5x+b. Trova “bbb”.
Isolando e risolvendo per bbb si ottiene:
Ricorda che bbb è anche nota come intercetta y, quindi anche l’intercetta y è 161616!
Trovare la pendenza da due punti
Questione 10: Dati due punti (6, 1) e (-10, 9), trovare la pendenza della retta.
Ricorda che per trovare la pendenza della retta, usiamo l’equazione della pendenza
Quindi usando questa formula si ottiene:
E se invece dobbiamo trovare l’intera equazione di una linea?
Equazione di una retta dati due punti
Questione 11: Dati due punti (-6, 1) e (2, 6), trovare l’equazione in forma di intercetta della pendenza.
In pratica stiamo cercando di trovare l’equazione nella forma di y=mx+by = mx + by=mx+b. Per fare questo, dobbiamo cercare mmm e bbb.
Ricordo che per trovare mmm, usiamo l’equazione della pendenza
Quindi usando questa formula si ottiene:
Ora abbiamo l’equazione
Ora dobbiamo cercare bbb. Per risolvere bbb, scegliamo uno dei punti dati e lo inseriamo nell’equazione. Possiamo farlo perché entrambi i punti giacciono sulla retta, e qualsiasi punto sulla retta soddisferebbe l’equazione. Usiamo il punto (2, 6). Vediamo che:
Isolando bbb si ottiene:
Mettendo questo in forma decimale, otteniamo che b=4.75b = 4.75b=4.75. Quindi, la nostra equazione in forma di intercetta di pendenza è:
L’ultima cosa da trattare in questa sezione è trovare il dominio e l’intervallo di una linea.
Come trovare dominio e intervallo?
Per trovare il dominio di una linea, ci stiamo sostanzialmente facendo questa domanda: cosa può essere xxx? Se xxx può essere quei valori, allora li aggiungiamo nel dominio.
La stessa cosa vale per il range. Cosa può essere yyy? Se yyy può essere quei valori, allora li aggiungiamo nel range. Facciamo un esempio.
Domanda 12: Trova il dominio e l’intervallo dell’equazione y=2x+1y = 2x + 1y=2x+1.
Nota che se disegniamo il grafico di questa linea, allora otterremo:
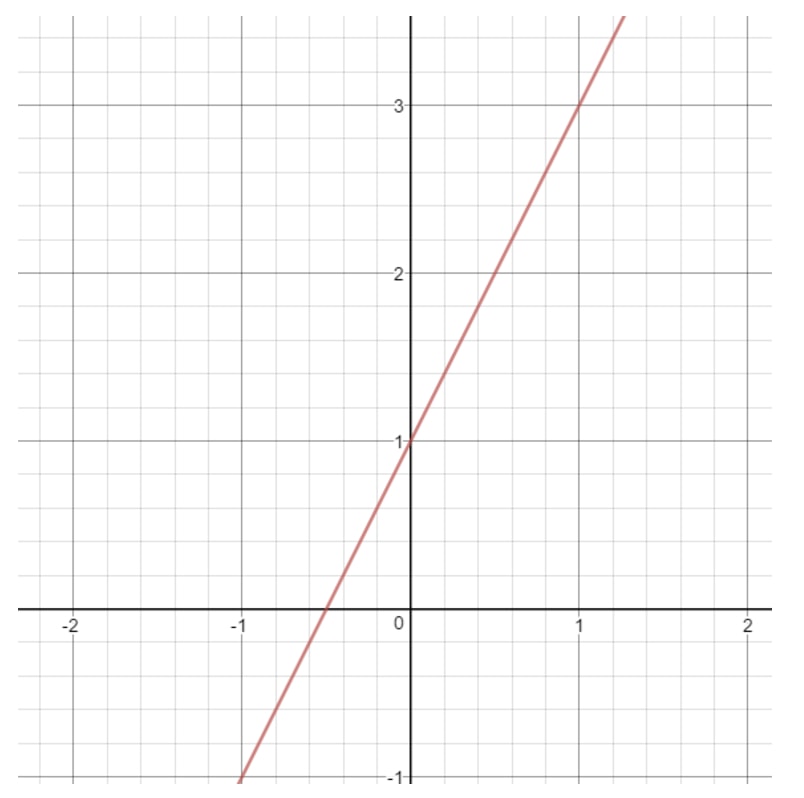
Cosa può essere xxx in questa linea? Notate che xxx può essere qualsiasi cosa perché con qualsiasi valore di xxx, possiamo ottenere un punto che è sulla linea. Lo stesso vale per y. Possiamo sempre scegliere un valore yyy che ci dia un punto su una linea. Quindi diciamo che
dove R significa “tutti i numeri reali”. Facciamone una più difficile.
Questione 13: Trova il dominio e l’intervallo dell’equazione y=-2y = -2y=-2.
Ora se tracciamo questa retta su un grafico, otterremo:
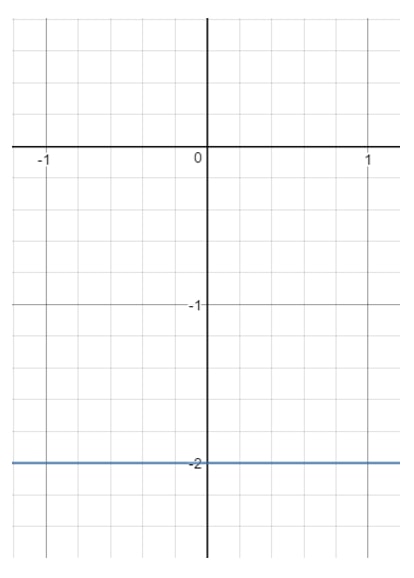
Notare che xxx può essere qualsiasi cosa perché con qualsiasi valore xxx, possiamo ottenere un punto che si trova sulla retta purché y=-2y = -2y=-2. Tuttavia, guardate yyy. Vedete che yyy è costretta a -2-2-2 e non può essere altro. Nel momento in cui si sceglie un altro valore di yyy (come 111), allora quel punto sarà fuori dalla linea. Quindi questo significa che:
Domanda 14: Trova il dominio e l’intervallo dell’equazione x=1x = 1x=1.
Ora se tracciamo questa linea su un grafico, otterremo:
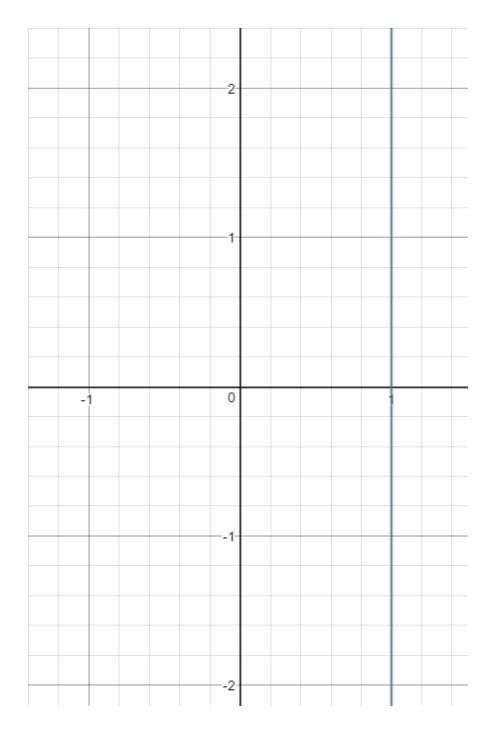
Vedi che xxx è costretto a 111 e non può essere altro. Nel momento in cui scegliete un altro valore di xxx (come 222), allora quel punto sarà fuori dalla linea.Tuttavia, guardate yyy. Notate che yyy può essere qualsiasi cosa perché con qualsiasi valore di yyy, possiamo ottenere un punto che si trova sulla linea purché x=1x = 1x=1
Quindi questo significa:
Se hai avuto molti problemi a disegnare i grafici per ottenere il dominio e l’intervallo, ti consiglio di usare questa calcolatrice.
https://www.desmos.com/calculator/2rnqgoa6a4
Ti insegna come fare il grafico di un’equazione lineare. Tutto quello che dovete fare è digitare i valori di mmm e bbb. Poi disegnerà automaticamente la linea per voi! Questo è anche utile quando stai cercando di trovare la forma dell’intercetta della pendenza.