Come calcolare la tensione nelle corde che sospendono un oggetto
Si può vedere nell’illustrazione sottostante che la forza, F, necessaria per sollevare l’oggetto è uguale al peso, W, dell’oggetto. Questa idea è il concetto fondamentale che sta alla base della nostra formula della forza di tensione. Di seguito è mostrato anche il diagramma a corpo libero dell’oggetto che mostra le forze di tensione, T, che agiscono nella corda. Come potete vedere, le forze di tensione vengono in coppia e in direzioni opposte:
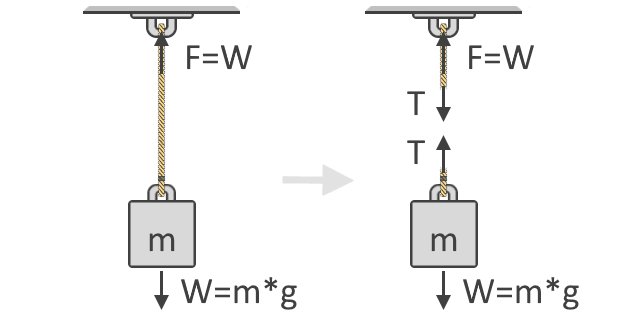
Seguendo la Seconda Legge del Moto di Newton, possiamo quindi esprimere la somma delle forze usando il diagramma a corpo libero dell’oggetto, come mostrato sul lato destro della figura sopra. Usiamo i diagrammi a corpo libero per mostrare le diverse direzioni e grandezze delle forze che agiscono su un corpo. In equilibrio, queste forze dovrebbero essere tutte uguali a zero. Considerando tutte le forze verso l’alto come positive e verso il basso come negative, la nostra equazione è:
ΣF = 0 = T + (-W)T = W
dove il peso, W, diventa negativo poiché è diretto verso il basso. Trasponendo W sull’altro lato dell’equazione, possiamo ora vedere che la forza di tensione nella corda è uguale al peso dell’oggetto che porta, come mostrato anche sopra.
Se usiamo più corde per sollevare l’oggetto, la forza di tensione totale viene divisa nelle corde. La forza di tensione in ogni corda dipende dai loro angoli rispetto alla direzione della forza a cui si oppone. Per capire meglio, consideriamo un altro diagramma a corpo libero di un oggetto sospeso con due corde, come mostrato qui sotto:
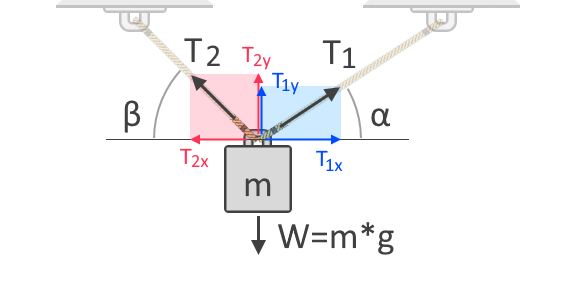
Nel diagramma a corpo libero mostrato sopra, possiamo vedere le componenti orizzontale e verticale delle forze di tensione, T₁ e T₂. Le forze sono vettori, il che significa che hanno sempre sia la grandezza che la direzione. Come tutti i vettori, le forze possono essere espresse in queste componenti che danno l’influenza della forza lungo gli assi orizzontale e verticale. T₁ₓ e T₂ₓ sono le componenti verticali di T₁ e T₂, rispettivamente. D’altra parte, T₁ᵧ e T₂ᵧ sono le componenti verticali delle stesse forze, rispettivamente. Poiché la gravità agisce sull’oggetto sull’asse verticale, dobbiamo considerare le componenti verticali delle forze di tensione per la nostra sommatoria di forze come segue:
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Poiché conosciamo anche gli angoli delle forze di tensione, possiamo esprimere T₁ᵧ e T₂ᵧ in termini di T₁ e T₂, rispettivamente, con l’aiuto delle funzioni trigonometriche:
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
Possiamo anche dire che perché il sistema sia in equilibrio, l’oggetto non deve muoversi orizzontalmente o lungo l’asse x. Pertanto, le componenti orizzontali di T₁ e T₂ devono essere uguali a zero. Inoltre, con l’aiuto della trigonometria, possiamo esprimere T₁ₓ e T₂ₓ in termini di T₁ e T₂, rispettivamente:
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Se dividiamo entrambi i lati per cos(α), otteniamo un’equazione in cui T₁ è espressa in termini di T₂ e degli angoli:
T₁ = T₂ * cos(β) / cos(α)
Possiamo quindi utilizzare questa equazione per risolvere T₂ sostituendo T₂ * cos(β) / cos(α) come T₁ nella nostra equazione della somma delle forze, come mostrato di seguito:
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
Infine, se moltiplichiamo questa intera equazione per cos(β) / cos(α) come abbiamo derivato nel valore di T₁ in termini di T₂, e poi semplificando tutto, otteniamo questa equazione:
T₁ = W / * T₁ = W / * T₁ = W /
Ora basta conoscere gli angoli delle corde di tensione rispetto all’orizzontale. Se viene dato un angolo dalla verticale, basta sottrarre questo angolo da 90°. Così facendo si ottiene l’angolo rispetto all’orizzontale. Tuttavia, se vi vengono dati altri valori di angoli che possono essere maggiori di 90° o anche di 180°, potreste voler controllare il nostro calcolatore di angoli di riferimento per aiutarvi a determinare l’angolo di cui avete bisogno. Dopo aver determinato i valori delle variabili nelle nostre formule delle forze di tensione, possiamo ora risolvere le forze di tensione.