Come la luce riflette o trasmette da una struttura materiale c’è un cambiamento di polarizzazione. L’elissometria misura questa risposta che dipende dalle proprietà ottiche e dallo spessore dei singoli materiali. L’elissometria è usata principalmente per determinare le costanti ottiche e lo spessore del film, ma anche per caratterizzare la composizione, la cristallinità, la rugosità, la concentrazione di drogaggio e altre proprietà del materiale associate a un cambiamento nella risposta ottica.

Le aree di applicazione sono la ricerca di base nelle scienze fisiche, i semiconduttori e le soluzioni di archiviazione dati, gli schermi piatti, la comunicazione, i biosensori e le industrie di rivestimento ottico. L’elissometria ha anche la flessibilità di misurare la maggior parte dei tipi di materiali: dielettrici, semiconduttori, metalli, superconduttori, organici, rivestimenti biologici e compositi.

Definizione di luce polarizzata

La luce può essere descritta come un’onda elettromagnetica che viaggia nello spazio. Il modo in cui il campo di un’onda elettromagnetica si comporta in relazione allo spazio e al tempo è chiamato polarizzazione. La luce è considerata non polarizzata quando il suo orientamento e la sua fase sono totalmente arbitrari. L’elissometria, tuttavia, misura la luce polarizzata – un campo elettrico che segue un percorso specifico e ha una forma distinta in qualsiasi punto. Un’onda elettromagnetica che viaggia in direzione z può essere descritta dalle sue componenti x e y, perché il suo campo elettrico è sempre ortogonale alla direzione di propagazione. Quando due onde luminose ortogonali sono in fase, la luce risultante è polarizzata linearmente. Il suo orientamento è determinato dalle ampiezze relative. La luce è considerata polarizzata circolarmente se le onde ortogonali sono fuori fase di 90° e hanno la stessa ampiezza. La polarizzazione più comune è ellittica e combina onde ortogonali di ampiezza e fase arbitrarie. È da qui che l’ellissometria prende il suo nome.

Diversi tipi di polarizzazione:

Lineare

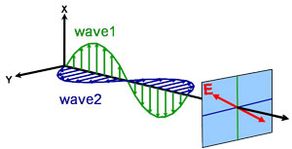
Circolare

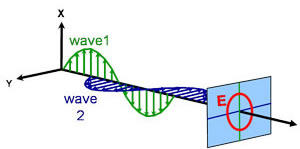
Elittica

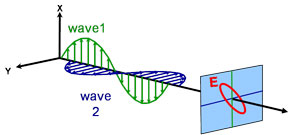
Proprietà ottiche

Le proprietà ottiche che determinano come la luce interagisce con un materiale sono descritte da due valori. Sono generalmente rappresentati come un numero complesso. L’indice di rifrazione complesso (ñ) consiste nell’indice (n) e un coefficiente di estinzione (k):

Le proprietà ottiche possono anche essere rappresentate come una funzione dielettrica complessa:

con la seguente relazione tra convenzioni:

L’indice rappresenta la velocità di fase della luce quando viaggia in un materiale rispetto alla velocità della luce quando viaggia nel vuoto, c:

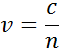
Quando entra in un materiale con un indice maggiore, la luce rallenta. Poiché la frequenza delle onde luminose non cambia, la lunghezza d’onda si accorcia. La perdita di energia dell’onda nel materiale è descritta dal coefficiente di estinzione che è legato al coefficiente di assorbimento come segue:

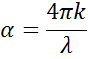
Secondo la legge di Beer, la luce perde intensità in un materiale assorbente. Il coefficiente di estinzione dimostra quanto velocemente la luce scompare in un materiale.

La figura 4 mostra un’onda luminosa che viaggia attraverso due diversi materiali di diverse proprietà prima di tornare nell’ambiente.

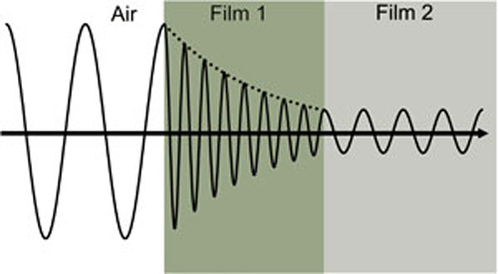
Figura 4: Onda luminosa che viaggia dall’aria nella pellicola assorbente 1 e poi nella pellicola trasparente 2. La velocità di fase e la lunghezza d’onda cambiano in entrambi i materiali a seconda dell’indice di rifrazione (Film 1: n=4, Film 2: n=2).

La lunghezza d’onda determina le costanti ottiche. La figura 5 mostra le costanti ottiche per TiO2 dall’UV all’IR. A causa dei diversi processi che traggono energia dall’onda luminosa, l’assorbimento (k>0) avviene sia nell’UV che nell’IR. L’assorbimento IR è solitamente causato da vibrazioni molecolari o foniche o da portatori liberi. L’assorbimento UV avviene generalmente a causa di transizioni elettroniche, dove l’energia luminosa eccita gli elettroni a stati elevati. La figura 5 mostra che le costanti ottiche ipotetiche o reali non sono indipendenti, ma collegate matematicamente attraverso le relazioni di Kramers-Kronig.

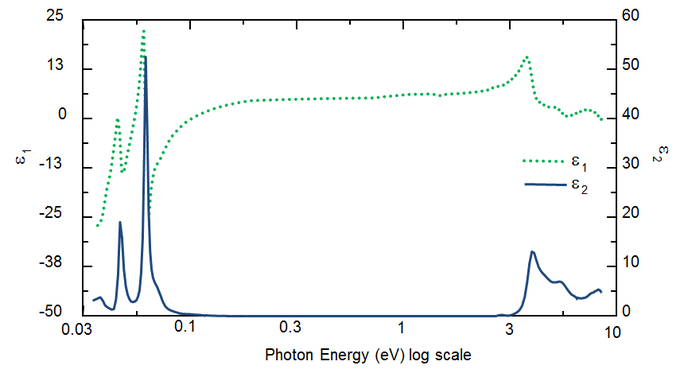
Figura 5: Funzione dielettrica complessa per film di TiO2 con lunghezze d’onda da IR (piccolo eV) a UV (alto eV).

Interazione tra luce e materiali

Quando la luce interagisce con un materiale questo porta a condizioni limite all’interfaccia. Durante questo, le equazioni di Maxwell devono essere sempre soddisfatte. La figura seguente mostra come la luce incidente riflette e rifrange all’interfaccia. L’angolo tra il raggio incidente e la normale del campione (θi) sarà uguale all’angolo riflesso (θr). La luce che entra in un materiale viene rifratta con un angolo θt dato da:

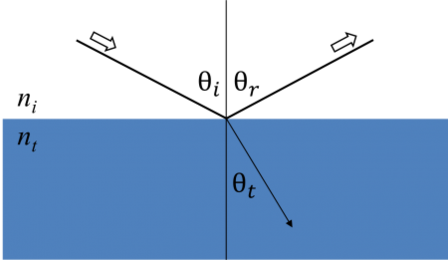
Figura 6: La luce riflette e rifrange secondo la legge di Snell.

Ad ogni interfaccia una parte della luce viene riflessa mentre il resto trasmette all’angolo rifratto. A seconda delle condizioni al contorno, si applicano soluzioni diverse per i campi elettrici paralleli e perpendicolari alla superficie del campione. La luce può quindi essere separata in componenti ortogonali rispetto al piano di incidenza (polarizzata p e s). Entrambe le componenti possono essere calcolate separatamente. Ecco come Fresnel ha descritto la quantità di luce riflessa e trasmessa ad un’interfaccia tra materiali:

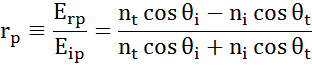
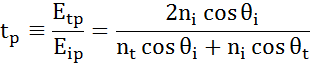
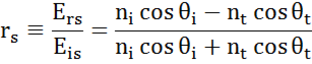
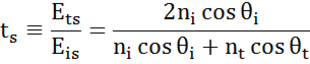
Interfacce multiple con appropriati coefficienti di riflessione e trasmissione di Fresnel si verificano con film sottili e strutture multistrato. Per definire correttamente il fascio riflesso o trasmesso, la fase relativa di ogni componente della luce deve essere seguita. Lo spessore di fase del film è quindi determinato come segue:

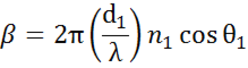
Quando diverse onde luminose si sovrappongono, si verifica un’interferenza che dipende dalla fase relativa di ogni singola onda luminosa. La figura seguente mostra la combinazione di onde luminose nel fascio riflesso e i loro corrispondenti calcoli di Fresnel.

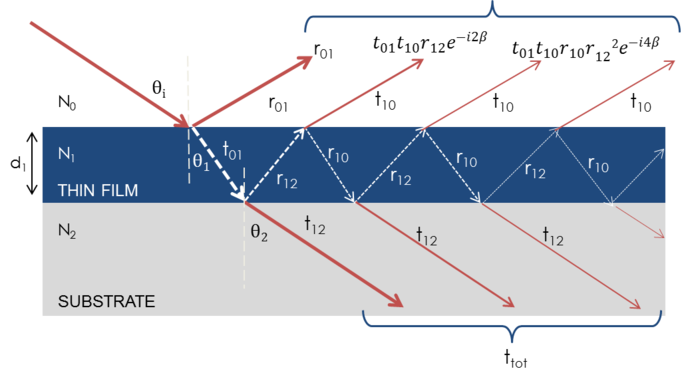
Figura 7: La luce riflette e rifrange ad ogni singola interfaccia, il che porta a fasci multipli in un film sottile. L’interferenza dei fasci dipende dalla fase relativa e dall’ampiezza dei campi elettrici. La reazione del fascio può essere calcolata con i coefficienti di riflessione e trasmissione di Fresnel.

Misurazioni

L’elissometria misura principalmente come i componenti p e s reagiscono l’uno rispetto all’altro durante la riflessione o la trasmissione. Quindi un raggio di riferimento fa sempre parte dell’esperimento. Una polarizzazione nota viene riflessa o trasmessa dal campione e si misura la polarizzazione in uscita. Il cambiamento di polarizzazione è la misura dell’ellissometria:

La figura 6 mostra una tipica misura di ellissometria del campione. La luce incidente lineare ha sia componenti p che s. La luce riflessa mostra sia cambiamenti di ampiezza che di fase per la luce polarizzata p e s. Questi cambiamenti sono misurati dall’ellissometria.

Per raccogliere i dati dell’ellissometria sono necessari: sorgente luminosa, generatore di polarizzazione, campione, analizzatore di polarizzazione e rilevatore. Sia il generatore di polarizzazione che l’analizzatore sono costituiti da parti ottiche che manipolano la polarizzazione: compensatori, polarizzatori e modulatori di fase. Le configurazioni tipiche dell’ellissometro incorporano un analizzatore rotante (RAE), un polarizzatore rotante (RPE), un compensatore rotante (RCE) e una modulazione di fase (PME). La figura qui sotto mostra una configurazione RAE.

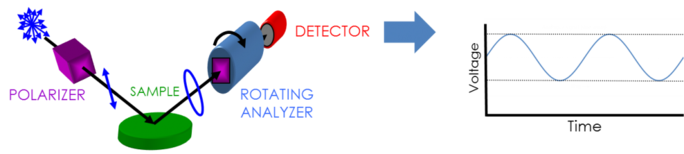
La luce non polarizzata è prodotta da una sorgente luminosa e poi inviata attraverso un polarizzatore. Il polarizzatore è impostato per far passare solo la luce con un certo orientamento del campo elettrico. Poiché l’asse del polarizzatore è allineato tra i piani p e s, entrambi raggiungono la superficie del campione. La luce ora polarizzata linearmente viene riflessa dalla superficie del campione diventando così polarizzata ellitticamente, e quindi inviata attraverso un polarizzatore a rotazione continua (l'”analizzatore”). La quantità di luce che può attraversare dipende dall’orientamento del polarizzatore rispetto all’ellisse del campo elettrico del campione. Per definire la polarizzazione riflessa, la luce viene convertita in un segnale elettronico nel rilevatore. Confrontando questi dati con la polarizzazione d’ingresso stabilita, si ottengono informazioni sul cambiamento causato dalla riflessione del campione: la misura ellissometrica di Psi e Delta.

Analisi dei dati

L’elissometria è usata per definire lo spessore del film di materiale o le costanti ottiche misurando i cambiamenti di polarizzazione della luce. Le costanti ottiche “pseudo” dalla misurazione ellissometrica possono essere derivate invertendo i dati determinati per una singola riflessione. Questo è utile per il materiale sfuso.

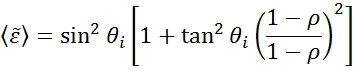
L’equazione di cui sopra non conta con nessuno strato superficiale. Tuttavia, normalmente c’è un ossido o una rugosità superficiale nei materiali sfusi. Un’inversione diretta includerà questi dati come parte delle costanti ottiche di massa. Vedere la fig. 10 per una panoramica di un tipico processo di analisi dei dati utilizzato nelle misurazioni ellissometriche. Poiché non è possibile scrivere un’equazione esatta, è necessaria un’analisi di regressione. La risposta è spesso sovradeterminata con solo poche incognite e centinaia di punti di dati sperimentali. Un’analisi di regressione permette di includere tutti i dati misurati per determinare la soluzione.

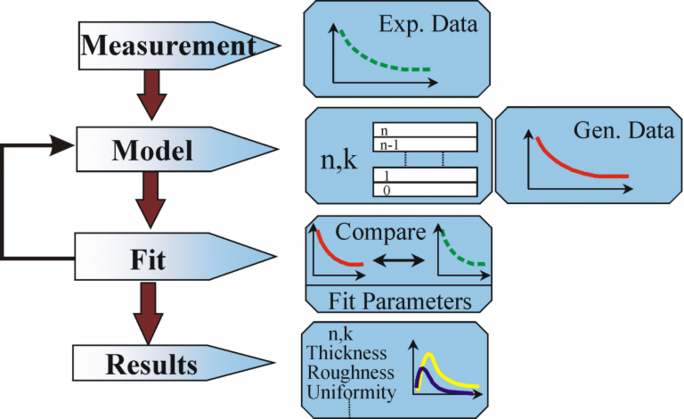
Figura 10: Diagramma di flusso per l’analisi dei dati dell’ellissometria.

La seguente procedura è usata per l’analisi dei dati: il campione è misurato e un modello è fatto del campione. Con l’aiuto di questo modello vengono calcolati i risultati presunti dalle equazioni di Fresnel, che descrivono lo spessore e le costanti ottiche di ogni materiale. Viene fatta una valutazione del calcolo preliminare, se questi valori sono sconosciuti. I valori calcolati sono confrontati con i dati sperimentali. Per far corrispondere meglio i dati sperimentali e di calcolo, i dati sconosciuti del materiale possono essere variati. Tuttavia, i punti dei dati sperimentali dovrebbero sempre essere più dei parametri sconosciuti. Per esempio, al massimo due proprietà del materiale possono essere determinate con un ellissometro a lunghezza d’onda singola, poiché produce esattamente due punti dati: Ψ, Δ (Psi e Delta). La regressione viene usata per trovare la migliore corrispondenza tra modello ed esperimento. La differenza tra le curve dei dati è quantificata con l’aiuto di uno stimatore come l’errore quadratico medio (MSE). Le proprietà sconosciute sono variate fino a raggiungere il minimo MSE. Questo significa che l’MSE più basso equivale alla risposta migliore.

Vedi la figura qui sotto per la curva MSE contro lo spessore del film per un film trasparente su silicio. Il valore più basso di MSE si verifica ad uno spessore di 749 nm, nonostante un certo numero di minimi locali. Quindi anche lo spessore corretto del film è 749 nm. L’algoritmo di regressione potrebbe considerare un minimo locale come corretto. Quindi, per determinare il minimo globale corretto è saggio confrontare i risultati a occhio per il più basso MSE.

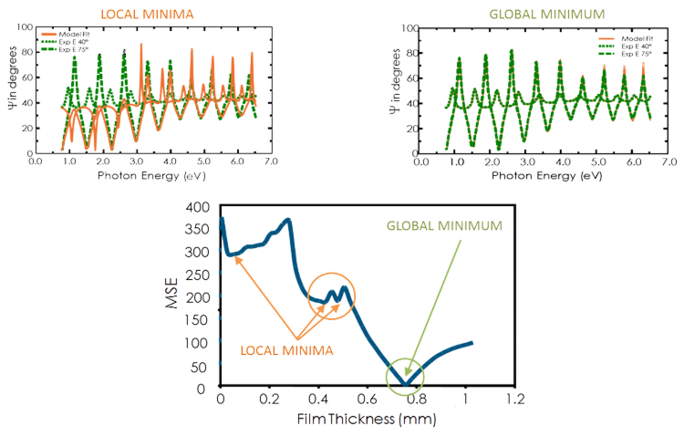
Figura 11, in alto a destra: Dati sperimentali e curve corrispondenti generate per il modello al minimo globale. Figura 11, in alto a sinistra: Una curva simile al minimo locale vicino a uno spessore di 0,45 µm può essere facilmente identificata come risultato errato. Figura 11, in basso: La curva MSE in funzione dello spessore mostra il minimo globale. Un algoritmo di regressione può dare i minimi locali, ma non il risultato finale.

Determinazione dello spessore del film

Lo spessore del film è solitamente determinato dall’interferenza tra la luce che riflette dalla superficie e la luce che attraversa il film. Se questa interferenza è considerata costruttiva o distruttiva dipende dalla fase relativa della luce che si unisce alla riflessione superficiale. L’interferenza include sia informazioni di ampiezza che di fase. L’informazione di fase da Δ è molto sensibile ai film fino allo spessore sub-monolayer. Vedere la figura seguente per un confronto tra l’intensità riflessa e l’ellissometria per la stessa serie di strati sottili di SiO2 su Si. La riflettanza per ogni film è quasi la stessa mentre ci sono grandi variazioni in Δ.

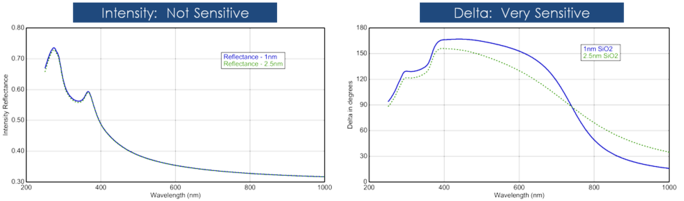
Figura 12, a sinistra: Intensità riflessa e delta ellissometrico (destra) per due ossidi sottili su silicio. La misura dell’intensità non mostra che il Delta è altamente sensibile ai film di scala nanometrica.

L’ellissometria è comunemente usata per film da sub-nanometri a pochi micron di spessore. Con film più spessi di alcune decine di micron, le oscillazioni di interferenza possono essere risolte solo con difficoltà crescente, tranne quando si usano lunghezze d’onda infrarosse più lunghe. Questo è il motivo per cui per i film più spessi si usano normalmente altre tecniche di misurazione.

Per misurare lo spessore, una parte della luce deve viaggiare attraverso l’intero film e poi tornare alla superficie. Con i materiali che assorbono la luce, le misure ottiche dello spessore possono essere eseguite solo su strati sottili e semi-opachi, a meno che non vengano eseguite su regioni spettrali con meno assorbimento. Per esempio, un film organico che assorbe la luce UV e IR può essere trasparente alle lunghezze d’onda del visibile medio. I metalli assorbono fortemente a tutte le lunghezze d’onda, quindi lo spessore massimo dello strato che può essere determinato è di circa 100 nm.

Costanti ottiche

Le costanti ottiche giocano un ruolo importante per le misure di spessore. Lo spessore di un film influenza la lunghezza del percorso della luce che viaggia attraverso il film, l’indice determina la velocità dell’onda luminosa e l’angolo di rifrazione. Entrambi contribuiscono quindi al ritardo tra la luce che viaggia attraverso il film e la riflessione della superficie. È necessario stabilire n e k così come lo spessore per ottenere risultati corretti da una misurazione ottica.

Poiché le costanti ottiche di un materiale variano per diverse lunghezze d’onda, tutte le lunghezze d’onda che vengono analizzate con l’ellissometro devono essere determinate individualmente. La risposta di un materiale ad ogni lunghezza d’onda può essere anticipata utilizzando una tabella di costanti ottiche. Per evitare la minuziosa regolazione delle costanti ottiche sconosciute lunghezza d’onda per lunghezza d’onda, è preferibile utilizzare tutte le lunghezze d’onda contemporaneamente. I parametri regolabili di una relazione di dispersione, per esempio, permettono alla forma complessiva della costante ottica di corrispondere ai risultati sperimentali. Rispetto alla regolazione dei singoli valori n e k per ogni lunghezza d’onda, il numero di parametri liberi sconosciuti si riduce considerevolmente.

Le relazioni Cauchy o Sellmeier sono frequentemente usate per descrivere l’indice per materiali trasparenti dove la relazione Cauchy è normalmente data come:

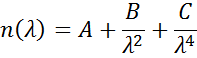
con i tre termini adattati per corrispondere all’indice di rifrazione del materiale. La relazione di Cauchy non è limitata dalla coerenza di Kramers-Kronig (KK) e può portare a dispersioni non fisiche. La relazione Sellmeier d’altra parte impone la coerenza di Kramers-Kronig (KK), che assicura che la dispersione ottica mantenga una forma realistica. La relazione Sellmeier è tipicamente scritta come:

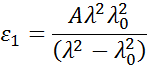
I materiali assorbenti hanno spesso una regione di lunghezza d’onda trasparente che può essere modellata con la relazione Cauchy o Sellmeier. Mentre la regione assorbente, tuttavia, deve tenere conto delle costanti ottiche sia reali che immaginarie. Per descrivere l’assorbimento per vari materiali, molte relazioni di dispersione utilizzano la teoria degli oscillatori, tra cui Lorentz, Harmonic e Gauss. Tutte condividono attributi simili con le caratteristiche di assorbimento che vengono descritte con l’ampiezza, l’allargamento e l’energia centrale (legata alla frequenza della luce). La forma della componente reale è calcolata usando la coerenza di Kramers-Kronig dopo che il comportamento immaginario è descritto dall’oscillatore. Per includere un possibile assorbimento extra oltre la regione spettrale misurata, viene aggiunto un offset alla componente reale. L’oscillatore di Lorentz può essere scritto come:

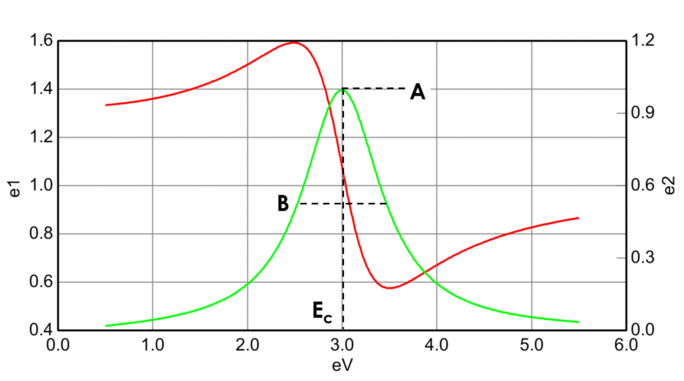
La figura 13 mostra anche l’ampiezza (A), l’allargamento (B), l’energia centrale (Ec) e l’offset (e1, off set) per un tipico oscillatore di Lorentz. L’energia E è legata alla frequenza di un’onda, n:

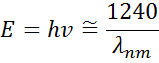
La costante di Planck h e la lunghezza d’onda λ sono date in nanometri. Altri modelli di dispersione, come Tauc-Lorentz e Cody-Lorentz, incorporano termini per descrivere l’energia del bandgap.

Altre letture

L’elissometria è una tecnica ottica consolidata per la misurazione di film sottili e materiali sfusi. Utilizza i cambiamenti di polarizzazione causati dalla riflessione/trasmissione dalla struttura di un materiale per determinare le caratteristiche del materiale come lo spessore e le costanti ottiche.

Aspnes D.E. (1985). La determinazione accurata delle proprietà ottiche tramite elipsometria. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. e Bashara N.M. (1987). Ellipsometria e luce polarizzata, Elsevier Science B.V., Amsterdam, The Netherlands.

Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). “Atti della seconda conferenza internazionale sull’ellissometria spettroscopica”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., e Redondo A. (1995). “Recenti applicazioni di ellissometria e spettroellissometria in sistemi elettrochimici”, In: I. Rubinstein (ed.), Elettrochimica fisica: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Diagnostica ottica per la lavorazione delle pellicole sottili, pp 425-479. Academic Press, San Diego, California.

Johs B. et al (1999). “Panoramica dell’elissometria spettroscopica ad angolo variabile (VASE), parte II: applicazioni avanzate”. Metrologia Ottica, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). “Sviluppi recenti nell’elissometria spettroscopica per applicazioni in situ”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. and Richter W. (1996). “Ellissometria spettroscopica” in: Bauer G e Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. and McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. e Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. e Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. and Snyder P.G. (1992). “Ellissometria spettroscopica ad angolo variabile” in: Brundle CR, Evans CA, and Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). “Panoramica dell’elissometria spettroscopica ad angolo variabile (VASE), parte I: teoria di base e applicazioni tipiche”. Metrologia Ottica, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). “Ellipsometria, Spettroscopia ad angolo variabile” in: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.