Varianssi on luku, joka ilmaisee, kuinka kaukana joukko lukuja on toisistaan.Varianssi on identtinen neliöllisen keskihajonnan kanssa ja ilmaisee siten ”samaa asiaa” (mutta voimakkaammin).

Varianssi – Esimerkki

Tutkimuksessa 100 henkilöä suorittaa yksinkertaisen nopeustehtävän 80 kokeilun aikana. Jokaiselta osallistujalta kirjataan siis 80 reaktioaikaa (sekunteina). Osa näistä tiedoista on esitetty alla.

Tällaisissa tutkimuksissa nähdään tyypillisesti, että ihmiset nopeutuvat, kun he suorittavat nopeustehtävän useammin. Toisin sanoen keskimääräisellä reaktioajalla on taipumus pienentyä kokeiden aikana.
Myös reaktioajat vaihtelevat tyypillisesti vähemmän eri ihmisten välillä sikäli, että he suorittavat tehtävää useammin. Teknisesti sanomme, että varianssi pienenee kokeiden aikana. Alla oleva taulukko havainnollistaa tätä kokeiden 1,4,7 ja 10 osalta.

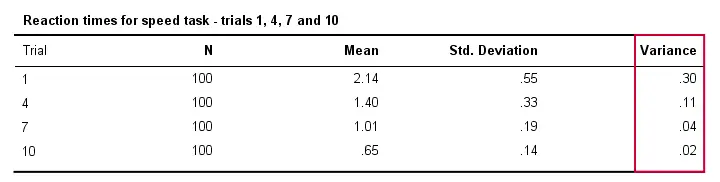
Varianssi ja histogrammi

Hyvä tapa havainnollistaa edellisen taulukkomme tiedot on histogrammi jokaisesta kokeesta. Näin alla oleva kuva havainnollistaa, että osallistujat nopeutuivat kokeiden myötä; kokeesta 1 kokeeseen 10 histogrammin pylväät siirtyvät vasemmalle, kohti 0 sekuntia.

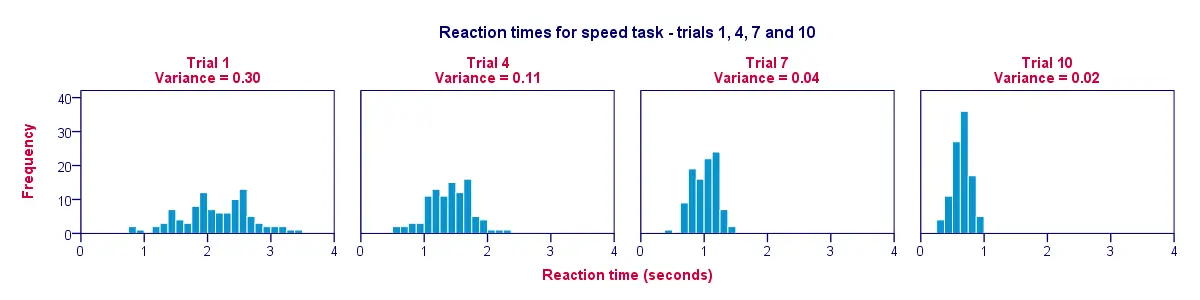
Toinen havainto on se, että histogrammit muuttuvat kapeammiksi (ja siten korkeammiksi) siirryttäessä kokeesta 1 kokeeseen 10; tämä havainnollistaa sitä, että reaktioajat vaihtelevat osallistujiemme välillä yhä vähemmän kokeen edetessä. Varianssi pienenee kokeiden aikana.

Varianssi – populaatiokaava

Varianssin laskemisen peruskaava on

$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$

Suosittelemme, että yrität ymmärtää, mitä tämä kaava tekee, koska se auttaa paljon ANOVA:n (= varianssianalyysi) ymmärtämisessä. Siksi demonstroimme sen pelkällä kourallisella dataa.

Varianssi – GoogleSheets

Yksinkertaisuuden vuoksi karsimme datamme ensimmäiseen kokeeseen ensimmäisten 5 osallistujan osalta. Nämä 5 reaktioaikaa -ja niiden varianssin laskeminen manuaalisesti- ovat tässä GoogleSheet-taulukossa.

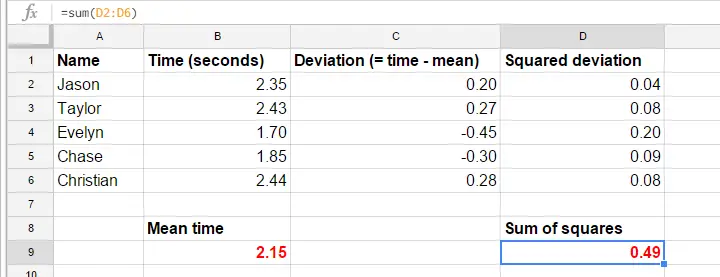
Varianssi – Laskentavaiheet

GoogleSheet-taulukon kaavoista näkee tarkkaan, miten varianssi lasketaan. Perusvaiheet ovat

1. laske keskimääräinen reaktioaika (2,15);
2. laske poikkeamapisteet (reaktioaika miinus keskimääräinen reaktioaika);
3. laske neliölliset poikkeamapisteet;
4. lisää neliölliset poikkeamapisteet. Tulos (0.49) on neliösumma, ANOVA:n tärkein rakennuspalikka;
5. jaa neliösumma havaintojen lukumäärällä (5 reaktioaikaa).

Vaihtoehtoisesti voit laskea varianssin kirjoittamalla =VARP(B2:B6) johonkin soluun (B2:B6 ovat soluja, joihin on tallennettu 5 reaktioaikaa). VARP on lyhenne sanoista ”varianssipopulaatio”. OpenOffice ja MS Excel sisältävät samankaltaisia kaavoja.

Varianssi – otoskaava

Samoin kuin keskihajonta, jos tietomme ovat yksinkertainen satunnaisotos paljon suuremmasta populaatiosta, edellä mainittu kaava aliarvioi systemaattisesti populaation varianssia. Tällöin käytämme hieman erilaista kaavaa:

$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$$

Mitä kaavaa käytämme, riippuu siis aineistostamme: sisältävätkö ne koko populaation, jota haluamme tutkia, vai ovatko ne pelkkä otos tästä populaatiosta?
Koska 100 osanottajaamme ovat selvästikin otos, käytämme otoksen kaavaa. GoogleSheetsissä kirjoittamalla =VAR(B2:B6) johonkin soluun saamme takaisin otoksen varianssin.

Varianssi SPSS:ssä

Sikäli kuin tiedämme, populaatiovarianssin kaava puuttuu kokonaan SPSS:stä, ja pidämme tätä vakavana puutteena. Sen sijaan SPSS käyttää aina otoksen kaavaa. tämä koskee sekä koehenkilöiden välistä varianssia (jota käsitellään tässä opetusohjelmassa) että koehenkilöiden sisäistä varianssia. Asiaankuuluvat tulosteet on esitetty alla.

Tämän tulostetaulukon osalta kannattaa myös huomata, että varianssi on tosiaan neliöity keskihajonta (pyöristämistä lukuun ottamatta).

Varianssin osalta se on siinä. Toivottavasti tämä opetusohjelma auttoi sinua ymmärtämään, mitä varianssi on.