Epäsuotuisa konvoluutio on analogisen tiedonsiirron luontainen ongelma. Esimerkiksi kaikki seuraavat asiat voidaan mallintaa konvoluutiona: kuvan epätarkkuus tärisevässä kamerassa, kaiku kaukopuheluissa, analogisten antureiden ja elektroniikan rajallinen kaistanleveys jne. Dekonvoluutio on prosessi, jossa signaalia suodatetaan ei-toivotun konvoluution kompensoimiseksi. Dekonvoluution tavoitteena on palauttaa signaali sellaiseksi kuin se oli ennen konvoluutiota. Tämä edellyttää yleensä, että konvoluution ominaisuudet (eli impulssi- tai taajuusvaste) tunnetaan. Tämä voidaan erottaa sokeasta dekonvoluutiosta, jossa parasiittisen konvoluution ominaisuuksia ei tunneta. Sokea dekonvoluutio on paljon vaikeampi ongelma, johon ei ole yleistä ratkaisua, ja lähestymistapa on räätälöitävä kulloisenkin sovelluksen mukaan.

Dekonvoluutiota on lähes mahdoton ymmärtää aika-alueella, mutta se on melko suoraviivaista taajuusalueella. Jokaisen alkuperäisen signaalin muodostavan sinimuotoisen signaalin amplitudia ja/tai vaihetta voidaan muuttaa, kun se läpäisee ei-toivotun konvoluution. Alkuperäisen signaalin erottamiseksi dekonvoluutiosuodattimen on kumottava nämä amplitudi- ja vaihemuutokset. Jos

esimerkiksi konvoluutio muuttaa sinimuotoisen signaalin amplitudia 0,5:llä ja sen vaihetta 30:llä asteella, dekonvoluutiosuodattimen on vahvistettava sinimuotoista signaalia 2,0:lla ja sen vaihetta 30:llä asteella.

Esimerkkinä dekonvoluution havainnollistamisesta käytämme gammasäteilyn ilmaisinta. Kuten kuvassa 17-3 on esitetty, tämä laite koostuu kahdesta osasta, skintillaattorista ja valoilmaisimesta. Sintillaattori on erityyppinen läpinäkyvä materiaali, kuten natriumjodidi tai vismuttigermanaatti. Nämä yhdisteet muuttavat jokaisen gammasäteilyn energian lyhyeksi näkyvän valon jaksoksi. Tämä valo

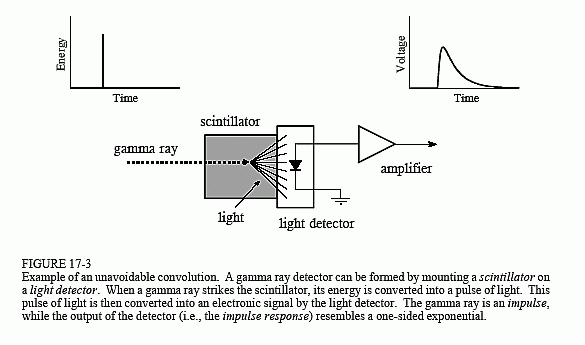
muunnetaan sitten elektroniseksi signaaliksi valodetektorilla, kuten fotodiodilla tai fotomonistinputkella. Jokainen ilmaisimen tuottama pulssi muistuttaa yksipuolista eksponentiaalia, jonka kulmat ovat hieman pyöristyneet. Tämä muoto määräytyy käytetyn tuikettajan ominaisuuksien mukaan. Kun agammasäde siirtää energiansa tuikettajaan, lähellä olevat atomit kiihottuvat korkeammalle energiatasolle. Nämä atomit räjähtävät satunnaisesti, ja kukin niistä tuottaa yhden näkyvää valoa tuottavan fotonin. Nettotuloksena on valopulssi, jonka amplitudi laskee muutamassa sadassa nanosekunnissa (natriumjodidin tapauksessa). Koska jokaisen gammasäteen saapuminen on impulssi, detektorin ulostulopulssi (eli yksipuolinen eksponentiaali) on järjestelmän impulssivaste.

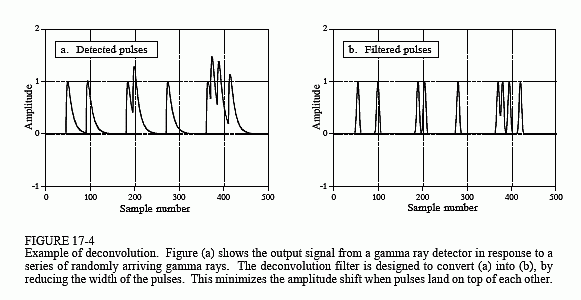
Kuvassa 17-4a on esitetty ilmaisimen tuottamat impulssit vastauksena satunnaisesti saapuviin gammasäteisiin. Tieto, jonka haluamme poimia tästä lähtösignaalista, on kunkin pulssin amplitudi, joka on verrannollinen sen synnyttäneen gammasäteilyn energiaan. Tämä on hyödyllistä tietoa, koska energia voi kertoa mielenkiintoisia asioita siitä, missä gammasäde on ollut. Se voi esimerkiksi antaa lääketieteellistä tietoa potilaasta, kertoa kaukaisen galaksin iän, havaita pommin lentokoneen matkatavaroissa jne.

Kaikki olisi hyvin, jos havaittaisiin vain satunnaisia gammasäteitä, mutta näin ei yleensä ole. Kuten kuvassa (a) näkyy, kaksi tai useampi pulssi voi mennä päällekkäin,jolloin mitattu amplitudi muuttuu. Yksi ratkaisu tähän ongelmaan on dekonvoluutioilmaisimen lähtösignaalin purkaminen, jolloin pulssit ovat kapeampia ja kasaantuminen vähenee. Ihannetapauksessa jokaisen pulssin haluttaisiin muistuttavan alkuperäistä impulssia. Kuten voitte epäillä, tämä ei ole mahdollista, ja meidän on tyydyttävä pulssiin, jonka pituus on rajallinen, mutta huomattavasti lyhyempi kuin havaittu pulssi. Tätä tavoitetta on havainnollistettu kuvassa 17-4b.

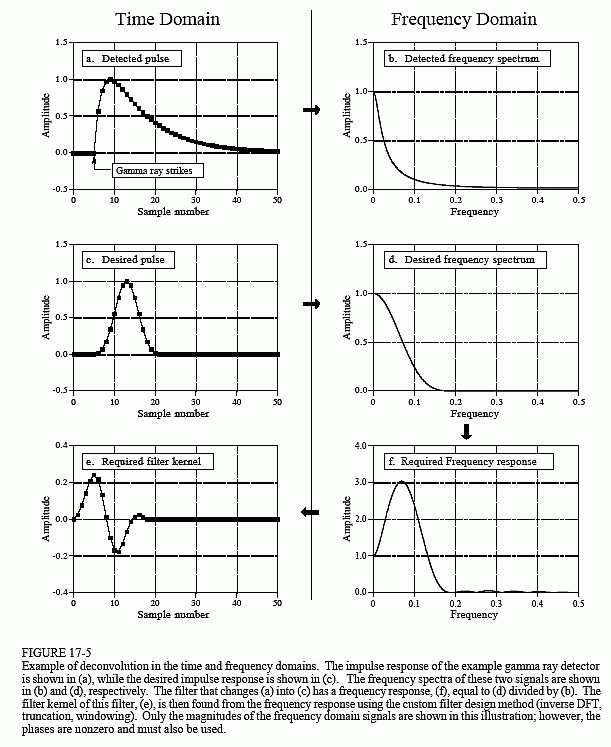
Vaikka havaintosignaalin informaatio on koodattu aika-alueella, suuri osa analyysistämme on tehtävä taajuusalueella, jossa ongelma on helpompi ymmärtää. Kuvassa 17-5a on ilmaisimen tuottama signaali(jotain, minkä tiedämme). Kuva (c) on signaali, jonka haluaisimme saada (myös jotain, minkä tiedämme). Tämä haluttu pulssi valittiin mielivaltaisesti samanmuotoiseksi kuin Blackmanin ikkuna, jonka pituus on noin kolmannes alkuperäisen pulssin pituudesta. Tavoitteenamme on löytää suodattimen ydin, (e), joka konvolvoituna (a) signaalin kanssa tuottaa (c) signaalin. Yhtälömuodossa: jos a * e = c, ja kun a ja c on annettu, löydä.

Jos nämä signaalit yhdistettäisiin yhteenlaskulla tai kertolaskulla konvoluution sijasta, ratkaisu olisi helppo: vähennyslasku käytetään ”vähentämään yhteenlaskua” ja jako käytetään ”vähentämään kertolaskua”. Konvoluutio on erilainen; ei ole olemassa yksinkertaista käänteisoperaatiota, jota voidaan kutsua ”dekonvoluutioksi”. Konvoluutio on liian sotkuinen, jotta se voitaisiin kumota manipuloimalla suoraan aikatason signaaleja.

Onneksi tämä ongelma on yksinkertaisempi taajuusalueella. Muista,että konvoluutio yhdellä alueella vastaa kertolaskua toisella alueella. Viitaten jälleen kuvan 17-5 signaaleihin: jos b × f = d, ja kun b ja d on annettu, etsitään f. Tämä ongelma on helppo ratkaista: suodattimen taajuusvaste (f) on halutun pulssin (d) taajuusspektri jaettuna havaitun pulssin (b) taajuusspektrillä. Koska havaittu pulssi on epäsymmetrinen, sen vaihe on nollasta poikkeava. Tämä tarkoittaa, että on käytettävä kompleksijakoa (eli suuruus & vaihe jaettuna toisella suuruus & vaiheella). Jos olet unohtanut, luvussa 9 määritellään, miten yhden spektrin kompleksijako tehdään toisella spektrillä. Tarvittava suodatinydin, (e), löydetään sitten taajuusvasteesta mukautetulla suodatinmenetelmällä (IDFT, shift, truncate, &multiply by a window).

Konvoluutiolla saavutettavalla parannuksella on rajansa. Toisin sanoen, jos ryhdyt ahneeksi, asiat hajoavat. Ahneeksi tuleminen tarkoittaa tässä esimerkissä sitä, että halutusta pulssista yritetään tehdä liian kapea. Katsotaanpa, mitä tapahtuu. Jos halutusta pulssista tehdään kapeampi, sen taajuusspektrissä on oltava enemmän korkeataajuisia komponentteja. Koska näiden korkeataajuisten komponenttien amplitudi on havaitussa pulssissa hyvin pieni, suodattimella on oltava hyvin suuri vahvistus näillä taajuuksilla. Esimerkiksi (f) osoittaa, että joitakin taajuuksia on kerrottava kolminkertaisesti, jotta saadaan haluttu pulssi (c). Jos halutusta pulssista tehdään kapeampi, dekonvoluutiosuodattimen vahvistus on vielä suurempi korkeilla taajuuksilla.

Ongelmana on, että pienet virheet ovat tässä tilanteessa hyvin anteeksiantamattomia. Jos esimerkiksi jotakin taajuutta vahvistetaan 30:llä, vaikka tarvitaan vain 28:aa, dekonvoluutiosignaali on todennäköisesti sekaisin. Kun dekonvoluutio viedään suuremmalle suoritustasolle, ei-toivotun konvoluution ominaisuudet on ymmärrettävä tarkemmin ja täsmällisemmin. Reaalimaailman sovelluksissa on aina tuntemattomia tekijöitä, jotka johtuvat esimerkiksi elektronisesta kohinasta, lämpötilan vaihtelusta, laitteiden välisestä vaihtelusta jne. Nämä tuntemattomat tekijät rajoittavat dekonvoluution toimivuutta.

Vaikka ei-toivottu konvoluutio ymmärrettäisiin täydellisesti, dekonvoluution suorituskykyä rajoittaa silti yksi seikka: kohina. Esimerkiksi useimmat ei-toivotut konvoluutiot ovat alipäästösuodattimen muodossa, mikä vähentää signaalin korkeataajuisten komponenttien amplitudia. Dekonvoluutio korjaa tämän vahvistamalla näitä taajuuksia. Jos näiden komponenttien amplitudi kuitenkin alittaa järjestelmän luontaisen kohinan, näihin taajuuksiin sisältyvä informaatio menetetään. Sitä ei voida palauttaa millään signaalinkäsittelyllä. Se on kadonnut lopullisesti. Adios! Hyvästi! Sayonara! Tämän datan palauttaminen vain vahvistaa kohinaa. Ääritapauksessa joidenkin taajuuksien amplitudi voi laskea kokonaan nollaan. Tämä ei ainoastaan hävitä tietoa, vaan yrittää saada dekonvoluutiosuodattimen vahvistuksen näillä taajuuksilla äärettömäksi. Ratkaisu: suunnitellaan vähemmän aggressiivinen dekonvoluutiosuodatin ja/tai asetetaan rajoituksia sille, kuinka paljon vahvistusta sallitaan millä tahansa taajuudella.

Miten pitkälle voit mennä? Kuinka ahne on liian ahne? Tämä riippuu täysin ongelmasta, jota vastaan hyökkäät. Jos signaali käyttäytyy hyvin ja siinä on vähän kohinaa, voidaan luultavasti saada aikaan merkittävä parannus (ajattele 5-10-kertaa). Jos signaali muuttuu ajan mittaan, sitä ei ymmärretä erityisen hyvin tai se on kohinainen, et pärjää läheskään yhtä hyvin (1-2-kertainen parannus). Onnistunut dekonvoluutio edellyttää paljon testausta. Jos se toimii jollakin tasolla, yritä mennä pidemmälle; tiedät, milloin se hajoaa. Mikään määrä teoreettista työtä ei anna sinun ohittaa tätä toistuvaa prosessia.

Dekonvoluutiota voidaan soveltaa myös taajuusalueen koodattuihin signaaleihin. Klassinen esimerkki on kuuluisan oopperalaulajan Enrico Caruson (1873-1921) vanhojen äänitteiden restaurointi. Nämä nauhoitukset on tehty nykystandardeihin nähden hyvin alkeellisella laitteistolla. Merkittävin ongelma on äänen keräämiseen käytetyn pitkän äänitorven resonanssit. Aina kun laulaja sattuu osumaan johonkin näistä resonanssitaajuuksista, äänitteen äänenvoimakkuus kasvaa äkillisesti. Digitaalinen dekonvoluutio onparantanut näiden äänitteiden subjektiivista laatua vähentämällä

musiikin kovia kohtia. Kuvaamme vain yleisen menetelmän;yksityiskohtaisen kuvauksen löydät alkuperäisestä artikkelista: T. Stockham, T. Cannon, andR. Ingebretsen, ”Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, s. 678-692.

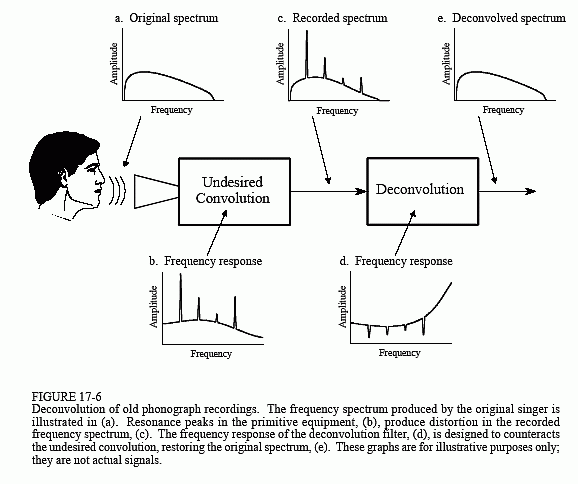
Kuvassa 17-6 esitetään yleinen lähestymistapa. Alkuperäisen audiosignaalin taajuusspektri on esitetty kuvassa (a). Kuvassa (b) esitetään äänityslaitteen taajuusvaste, joka on suhteellisen tasainen käyrä lukuun ottamatta useita teräviä resonanssipiikkejä. Tallennetun signaalin spektri, joka on esitetty kuvassa (c), on yhtä suuri kuin todellinen spektri (a) kerrottuna epätasaisella taajuusvasteella (b). Dekonvoluution tavoitteena on torjua epätoivottua konvoluutiota. Toisin sanoen dekonvoluutiosuodattimen taajuusvasteen (d) on oltava käänteisvaste (b):lle. Toisin sanoen jokainen huippu (b):ssä kumotaan vastaavalla notkahduksella (d):ssä. Jos tämä suodatin olisi suunniteltu täydellisesti, tulossignaalin spektri, (e), olisi identtinen alkuperäisen signaalin spektrin kanssa.

Tässä on juju: alkuperäinen tallennuslaite on jo kauan sitten hävitetty, ja sen taajuusvaste, (b), on arvoitus. Toisin sanoen kyseessä on sokea dekonvoluutio-ongelma; kun tiedossa on vain (c), miten voimme määrittää (d)?

Sokea dekonvoluutio-ongelmia käsitellään yleensä tekemällä arvio tai oletus tuntemattomista parametreista. Tämän esimerkin käsittelemiseksi oletetaan, että alkuperäisen musiikin keskiarvospektri vastaa nykylaulajan nykyaikaisella laitteistolla esittämän saman musiikin keskiarvospektriä. Keskimääräinen spektri löydetään luvussa 9 esitetyllä tekniikalla: signaali hajotetaan suureen määrään segmenttejä, jokaisesta segmentistä otetaan DFT, muunnetaan polaariseen muotoon ja keskiarvoistetaan sitten suuruudet yhdessä. Yksinkertaisimmassa tapauksessa tuntematon taajuusvaste on vanhan äänitteen keskimääräinen spektri jaettuna modernin äänitteen keskimääräisellä spektrillä. (Stockhamin ja muiden käyttämä menetelmä perustuu kehittyneempään tekniikkaan, jota kutsutaan homomorfiseksi prosessoinniksi ja joka antaa paremman arvion äänitysjärjestelmän ominaisuuksista).