Nolla on luku, joka sijoittuu suoraan lukujonon positiivisten ja negatiivisten lukujen väliin. Nollaa pidetään kokonaislukuna positiivisten luonnollisten lukujen (1, 2, 3, 4…) ja negatiivisten lukujen (…-4,-3,-2,-1) ohella.
Nolla on erityinen luku kokonaislukujen joukossa, sillä se on ainoa kokonaisluku, joka ei ole positiivinen eikä negatiivinen. Se on myös ainoa kokonaisluku, joka ei ole alkuluku eikä yhdistetty luku. Sitä pidetään parillisena lukuna, koska se on jaollinen kahdella ilman jäännöstä. Nolla on additiivinen identiteettielementti useissa algebran järjestelmissä, ja numeroa ”0” käytetään sijaisarvona lukujen esittämiseen tarkoitetuissa paikannimistöjärjestelmissä.
Nollalla on monia mielenkiintoisia ominaisuuksia, joiden vuoksi se kiinnostaa matemaatikkoja. Jos lisäät tai vähennät nollan mistä tahansa luvusta, luku pysyy samana Jos kerrot nollan millä tahansa luvulla, tulos on 0. Mikä tahansa nollan (0:nnen) potenssiin korotettu luku on 1, joten 20=1 ja 560=1. Perinteisessä algebrassa jakaminen 0:lla on määrittelemätöntä, joten mitään lukua ei voi jakaa 0:lla. Luku 0 on myös reaalilukujen ja kompleksilukujen alkuaine.
Luvun 0 historia
Miten ajatus nollasta syntyi? Nykyään se tuntuu meistä intuitiiviselta; nolla on luku, joka tarkoittaa nollamäärää – ei mitään. Näemme nollia kaikkialla yhteiskunnassa, ja ymmärrämme luonnollisesti, mitä ne tarkoittavat ja miten niitä voidaan käsitellä matemaattisesti. Historiallisesti ottaen nollan käsitteen yleistyminen matematiikan kohteeksi kesti kuitenkin melko kauan, ja monet ovat kautta historian väittäneet, että lukua nolla ei ole olemassa tai että ajatus nollasta on epäjohdonmukainen käsite.
Monilla muinaisilla yhteiskunnilla ei ollut eksplisiittistä käsitettä nollan määrästä tai tiettyä numeroa, jota olisi voitu käyttää sen esittämiseen. Muinaisilla egyptiläisillä ja babylonialaisilla oli molemmilla jonkinlainen käsitys nollasummasta ja tarve sijaisarvoille lukujen esittämisessä, mutta he eivät koskaan kehittäneet erillistä numeroa tai käsitettä edustamaan kyseistä määrää tai sijaisarvoa. Muinaisten egyptiläisten numerojärjestelmät olivat täysin kuvallisia, eikä niissä ollut paikka-arvoja, kun taas muinaiset babylonialaiset käyttivät numeroiden välisiä välilyöntejä paikka-arvojen esittämiseen.
Mayoilla oli selkeä nollan käsite, ja heillä oli erillinen numero, joka edusti tätä käsitettä ja jota he käyttivät paikka-arvona vigesimaalisessa kalenterijärjestelmässään (perusta 20). Vaikka maya-, olmec- ja muut esikolumbialaiset yhteiskunnat olivat historian ensimmäisten joukossa, joilla oli eksplisiittinen ja kehittynyt käsitys luvusta 0, nämä järjestelmät eivät kuitenkaan jatkaneet vaikutustaan vanhan maailman yhteiskuntiin Euroopassa.
Vanhoilla kreikkalaisilla sen sijaan oli monimutkainen suhde nollaan. Heillä ei ollut symbolia sen käsitteelle eikä sille sijaisarvona, koska he olivat epävarmoja siitä, voitiinko lukua 0 pitää aidosti olemassa olevana asiana. Miten, kysyivät he, jokin (luku) voisi olla ei mitään (nolla)? Kreikkalaisille luonnolliset luvut (1, 2, 3, 4, …) olivat peräisin ymmärryksestämme maailmassa olevista erillisistä yksittäisistä kohteista. Aristoteles itse väitti tunnetusti, että nollaa ei ole olemassa, sillä perusteella, että nolla edustaa tyhjyyttä tai ei-mitään, eikä aitoa tyhjyyttä tai ei-mitään voi olla olemassa.
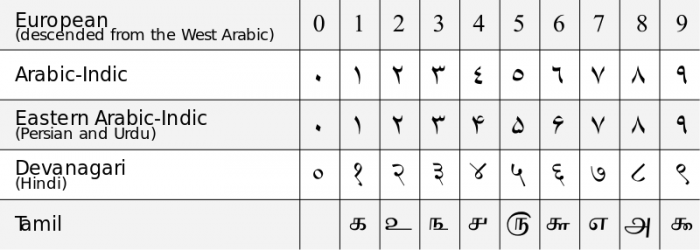
Kiinalaiset ymmärsivät ”nollan” sijaislukuna laskentajärjestelmissään, mutta he eivät pitäneet numeroa ”nollaa” minkään erillisen luvun edustajana, vaan ainoastaan käyttökelpoisena symbolina. Yleinen käsitys 0:sta erillisenä lukuna ja paikkamerkintäjärjestelmien numerona tuli Intiasta 6. vuosisadalla jKr. Intian matemaatikot kehittivät tuohon aikaan ensimmäiset kymmenjärjestelmän (base-10) merkintäjärjestelmät, jotka sisälsivät 0:n erillisenä numerona, ja heillä oli käsitys nollan ainutlaatuisista matemaattisista ominaisuuksista. Ajatus nollasta oli levinnyt Länsi-Eurooppaan 1100-luvulla jKr. Espanjassa Umayyad-kalifaatin alaisuudessa eläneiden islamilaisten matemaatikkojen vaikutuksesta, ja syntyi nykyaikainen arabiankielinen desimaalilukumerkintäjärjestelmä. Englanninkielisen sanan ”zero” ensimmäinen käyttö on vuodelta 1589.
Nollan matemaattiset ominaisuudet
Luvulla nolla on olennainen rooli lähes kaikilla matematiikan aloilla. Nolla on pienin ei-negatiivinen kokonaisluku, eikä sitä edistä mikään luonnollinen luku. Koska 0 on kokonaisluku, se on myös rationaaliluku, reaaliluku ja kompleksiluku. Matematiikassa 0:ta pidetään suureena, joka vastaa nollamäärää. Voidaan sanoa, että nolla on ”määrä”, joka on sellaisen joukon hallussa, jolla ei ole jäseniä.
Algebrassa
Alkeisalgebrassa nolla ilmaistaan usein siten, että se sijaitsee lukujonon keskellä. Lukua 0 pidetään parillisena lukuna, koska se on luvun 2 kokonaislukukerroin (2×0=0). 0 ei ole alkuluku, koska sillä on ääretön määrä tekijöitä, eikä se ole yhdistetty luku, koska mikään kahden alkuluvun tulo ei ole yhtä suuri kuin luku 0.
Luku 0 käyttäytyy neljän tärkeimmän aritmeettisen operaattorin (+, -, ×, ÷) ja eksponenttioperaation suhteen seuraavien sääntöjen mukaisesti:
- Lisäys: x+0=0+x=x. Nollaa pidetään additiivisena identiteettielementtinä, sillä mikä tahansa luku plus tai miinus nolla on yhtä suuri kuin kyseinen luku
- Subtraktio: x-0=x ja 0-x=-x
- Kerroinlasku: x⋅0=0⋅x=0. Mikä tahansa luku kertaa 0 on myös yhtä suuri kuin 0.
- Divisioona: 0/x=0, paitsi silloin kun x=0. x/0 on matemaattisesti määrittelemätön suure, koska 0:lla ei ole multiplikatiivista käänteislukua (mikään luku kertaa 0 ei anna 1:tä).
- Eksponentit: x0=1, paitsi silloin kun x=0. Pitkään on kiistelty siitä, onko 00 määrittelemätön vai hyvin muodostettu lauseke. Kaikille positiivisille x:lle 0x=0.
Rajoja koskevissa lausekkeissa suure 0/0 voi esiintyä rationaalifunktioiden raja-arvojen osoittamisen yhteydessä, kuten f(x)/g(x). Näissä tapauksissa 0/0 ei ole määrittelemätön vaan edustaa epämääräistä muotoa. Tämä ei tarkoita, että raja-arvo olisi määrittelemätön, vaan että se on laskettava muulla menetelmällä, kuten derivaatan avulla. On olemassa joitakin algebrallisia malleja, joissa jako nollalla antaa määritellyn suureen, kuten projektiivisesti laajennettu reaaliviiva tai Riemannin pallo.
joukkojen teoriassa
Joukkojen teoriassa luku 0 vastaa ”tyhjän joukon” tai ”nollajoukon” kardinaalisuutta (yleisesti esitetty muodossa {} tai {∅}. Joukon kardinaalisuus on joukon alkioiden määrä, jos joukossa ei ole yhtään appelsiinia, on joukko, jossa on 0 appelsiinia (appelsiinien tyhjä joukko).
Nollaa käytetään usein joukko-opissa lähtökohtana muiden luonnollisten lukujen rakentamisessa. Nämä von Neummanin konstruktiot, jotka on nimetty tunnetun polymaatikon John von Neumannin mukaan, rakentavat luonnolliset luvut määrittelemällä 0={} ja määrittelevät seuraajafunktion S(a) = a ∪ {a}. Luonnollisten lukujen kokonaisuus voidaan rakentaa seuraajafunktion rekursiivisista sovelluksista tyhjästä joukosta alkaen:
0 = {}
1 = 0 ∪ {0} = {0} = {{}}
2 = 1 ∪ {1} = {0,1} = {{}, {{}}}}
3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}}, {{}}, {{}}}}
ja niin edelleen. Tätä kaavaa seuraamalla voidaan rakentaa koko luonnollisten lukujen ääretön joukko. Näin voidaan sanoa, että jokaista luonnollista lukua vastaa joukko, joka sisältää kaikki sitä edeltävät luonnolliset luvut.
Fysiikassa
Kvantitatiivisten mittausten tekemisessä fysiikassa 0:ta pidetään lähtökohtana, josta kaikki muut yksiköiden mittaukset tehdään. Hyvin usein 0:n perusviiva vastaa jotakin fysikaalisesti merkittävää muuttujaa, joka on luonnollisesti erotettavissa kaikista muista mittaussuureista.
Esimerkiksi Kelvin-asteikolla lämpötila 0 K vastaa absoluuttista 0:aa – kylmintä lämpötilaa, joka on fysikaalisesti mahdollista. Celsius-asteikolla 0 °C määritellään veden jäätymispisteeksi ilmanpaineessa. Dynamiikan ja sähkömagnetismin yhteydessä arvo 0 annetaan tilanteelle, jossa systeemin potentiaalienergian määrä on mahdollisimman pieni. Esimerkiksi atomin perustilalle, atomin elektronien pienimmälle mahdolliselle energiatasolle, annetaan usein arvo 0.
Vastaavasti kinemaatiikan yhteydessä viitekehys, josta liikettä havainnoidaan, määritellään siten, että sen keskipiste sijaitsee koordinaattiakselin alkupisteessä pisteessä (0, 0). Kun kyseessä ovat säilyvät suureet, kuten massa-energia, impulssi ja kulmamomentti, säilyvien suureiden kokonaismuutos eristetyssä systeemissä on aina yhtä suuri kuin 0.
Tietotekniikassa
Tietokoneet tallentavat informaatiota bittien pituisina 1:ien ja 0:ien sarjoina. Tässä binäärisessä esityksessä 0 vastaa ”pois päältä”-asentoa ja vastakohtana on ”päällä”-asento, jota tarkoittaa 1. Arvo 0 sähköpiirissä tarkoittaa, että piiri on pois päältä eikä siinä ole sähkövirtaa. Vastaavasti monissa laskentalogiikoissa ”0” määritellään merkiksi, joka edustaa väärää totuusarvoa.
Tietokonetietokannoissa joukon elementit lasketaan nollaan perustuvaa laskentajärjestelmää käyttäen. Tämä tarkoittaa, että joukossa, jossa on n elementtiä, elementeillä on indeksit, jotka alkavat numerosta 0. Siten elementti, jonka indeksiluku on 0, on itse asiassa sarjan ensimmäinen elementti, ja indeksiluku 1 vastaa toista elementtiä ja niin edelleen. Yleisesti ottaen joukon n:nnen termin indeksiluku on n-1. Tämä laskentajärjestelmä voi aiheuttaa hämmennystä uusille ohjelmoijille, jotka ovat tottuneet antamaan intuitiivisesti indeksiluvut alkaen 1:stä.