Loimme ensimmäisen resistiivisen voimateorian rakeisille väliaineille, jotta voimme ennustaa voimia ja liikettä, koska se on samankaltainen kuin matalan Reynoldsin luvun uimarit nesteissä. Keskeinen ajatus on superpositioperiaate: rakeisessa väliaineessa mielivaltaista liikerataa pitkin liikkuviin monimutkaisen muotoisiin kappaleisiin ja jalkoihin kohdistuvat voimat voidaan approksimoida hyvin superpositiolla niiden kuhunkin elementtiin kohdistuvista voimista (kuva 1). Integraatioperiaate pätee pienen Reynoldsin uimareihin, koska koska inertiavaikutukset ovat merkityksettömiä, nesteen virtaus elementtien ympärillä on riittävän paikallista, jotta elementtiin kohdistuva rakeinen voima on riippumaton muihin elementteihin kohdistuvasta voimasta. Tämä huomioon ottaen oletimme, että resistiivisen voiman teoria toimisi myös rakeisille väliaineille.

Kuva 1. Resistiivisen voimateorian superpositioperiaate.
Resistiivisen voiman mittaukset
Koska eläimillä ja roboteilla on monimutkainen morfologia ja kinematiikka, niiden vartaloiden ja jalkojen kukin elementti voi olla eri syvyydellä, mutta niillä voi olla myös eri orientaatioita ja liikesuuntia (kuva 1, vasemmalla). Pienillä Reynoldsin luvuilla nesteissä uiville uimareille voidaan Stokesin laista johtaa, miten voima riippuu orientaatiosta ja suunnasta. Mutta rakeisten väliaineiden osalta emme tiedä, miten voima riippuu niistä, koska tällaisia yhtälöitä ei ole olemassa. Siksi teimme levyelementin avulla ensimmäiset mittaukset rakeisen aineen voimista tunkeutujan orientaation ja suunnan funktiona (kuva 1, oikea).
Havaitsimme, että voima (jännitys) riippuu herkästi sekä orientaatiosta että suunnasta (kuva 2, vasen). Pystysuora voima on suurin, kun levyn tunkeutuja on suuntautunut vaakasuoraan ja tunkeutuu alaspäin. Heti kun orientaatio poikkeaa vaakatasosta ja suunta poikkeaa alaspäin, pystysuora voima pienenee nopeasti.
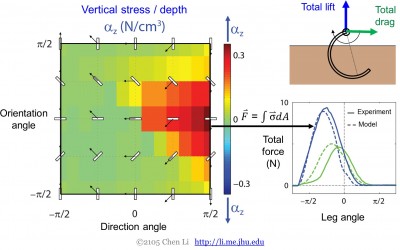
Kuva 2. Resistiivisen voiman mittaukset ja teorian validointi. Vain pystysuuntaiset resistiivisen voiman mittaukset on esitetty yksinkertaisuuden vuoksi.
Validointi resistiivisen voiman teoriasta
Rakeisen resistiivisen voiman mittaustulosten avulla integroimme jalkaterän elementteihin kohdistuvat jännitykset ja havaitsimme, että resistiivisen voiman teorialla voidaan hyvin ennustaa kokonaisnosto- ja -vetovoimat, jotka kohdistuvat robottijalkaan, jota liikutetaan rakeisen väliaineen halki (kuvio 2, oikealla). Superpositioperiaatteen ansiosta malli on tarkka muodoltaan ja liikeradaltaan mielivaltaisille jaloille:
Vastusvoimateorian ennustusvoima
Validoituamme vastusvoimateorian robottijalalla, jota pyöritettiin rakeisen väliaineen läpi (määrätty kinematiikka), testasimme seuraavaksi sen ennustusvoimaa robotilla, joka liikkuu vapaasti rakeisen väliaineen päällä. Ajoimme räätälöidyn jalkaisen robotin rakeisella väliaineella laajalla askeltaajuuden ja jalan kaarevuuden vaihteluvälillä. Kuten aiemmin totesimme, robotti liikkuu nopeammin jalkojen ollessa kuperalla pinnalla taaksepäin kuin eteenpäin:
Tämän jälkeen kehitimme robotille monirunkoisen dynaamisen simulaation ja käytimme resistiivisten voimien teoriaa laskeaksemme robotin runkoon ja jalkoihin kohdistuvat nosto- ja vetovoimat integroimalla elementtivoimat. Havaitsimme, että resistiivisen voimateorian avulla simuloinnilla ennustettu liikedynamiikka vastaa hyvin kokeellista havaintoa:
Kokeen ja simuloinnin vertailu osoitti, että resistiivisen voimateorian avulla pystytään ennustamaan jalkojen liikkuminen rakeisella väliaineella tarkasti ja nopeasti laajalla askeltaajuuden ja jalkojen kaarevuuden alueella (kuva 3).
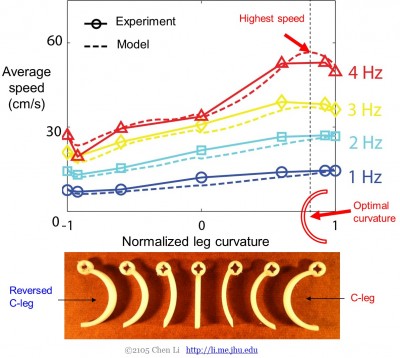
Kuva 3. Resistiivinen voimateoria ennustaa jalkaisen robotin liikkumisen rakeisella väliaineella.
Koska resistiivinen voimateoriamme mahdollisti voimien ja liikkumisen kvantitatiivisen ennustamisen rakeisella väliaineella analogisesti nesteiden aero- ja hydrodynamiikan kanssa, olemme luoneet ensimmäisen terradynamiikan virtaavalle maaperälle.
Vastusvoimateorian yleisyys
Toimme vastusvoimamittauksia erilaisille rakeisille väliaineille, joilla oli erilainen partikkelikoko, muoto, kitka, tiheys, tiivistyminen ja polydispersiteetti. Havaitsimme, että voiman riippuvuus tunkeutujan orientaatiosta ja suunnasta on hämmästyttävän samankaltainen (kuva 4, vasen).
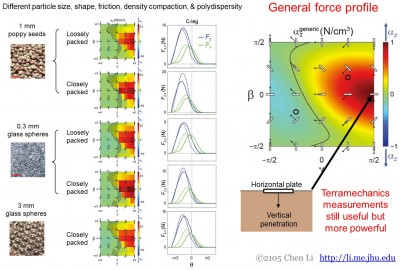
Kuva 4. Resistiivisen voimateorian yleisyys erilaisille rakeisille väliaineille ja sen käytännön hyöty.
Tästä on suuri käytännön hyöty. Koska näillä rakeisilla väliaineilla on sama yleinen jännitysprofiili, vain yksi voimamittaus maksimaalisen pystysuoran voiman määrittämiseksi riittää päättelemään voimat muiden suuntien ja suuntien osalta tarvitsematta mitata niitä kaikkia (kuva 4, oikealla). Tämä voidaan yksinkertaisesti tehdä tavallisella penetrometrillä. Tämä tarkoittaa myös sitä, että terramekaanisissa tutkimuksissa saatuja mittauksia, joissa käytetään alaspäin penetroivaa vaakasuoraa levyä, voidaan edelleen käyttää, mutta tehokkaammin resistiivisen voiman teoriaa käyttäen.
Viimeiseksi, superpositioperiaatteensa ansiosta resistiivisen voiman teoriaamme voidaan periaatteessa soveltaa eläimiin ja laitteisiin, joilla on mielivaltainen morfologia ja kinematiikka (edellyttäen, että ne toimivat alhaisen nopeuden, ei-inertiatason ja kontinuumin regiimissä). Havaitsimme esimerkiksi myös, että vastusvoimamittauksia vaakatasossa käyttävä teoria voi ennustaa hiekkakalaliskon liikkumisen rakeisessa väliaineessa.
Miksi klassinen terrämekaniikka epäonnistuu Mars Roversissa
Klassisessa terrämekaniikassa, koska suurilla pyörillä ja telaketjuilla on yleensä suhteellisen tasainen ja tasainen maanpinnan rajapinta, pystysuuntaiset tunkeutumisvoimat granulaarisessa väliaineessa luonnehtivat vain vaakasuoran levyn liikuttamista alaspäin (penetrometrin avulla) (kuva 5), mutta eivät tunkeutujaa muissa suunnissa ja orientaatioissa. Tätä käytetään sitten nosteen ennustamiseen, joka sitten tasapainotetaan (staattisesti ja dynaamisesti) ajoneuvon painon kanssa uppoamisen ennustamiseksi.
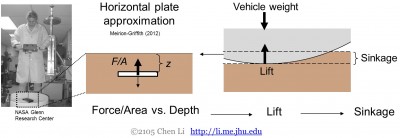
Kuva 5. Vaakasuoran levyn approksimaatio, joka on vallalla klassisten terramekaanisten mallien kehityksessä.
Mutta kun kyseessä ovat irtonaisella rakeisella väliaineella liikkuvien mönkijöiden pienet pyörät (tai jopa suuremmat pyörät, jotka on upotettu riittävän syvälle), maan rajapinta muuttuu erittäin kaarevaksi, ja sen suunta on kaukana vaakatasosta. Kuten olemme osoittaneet resistiivisen voiman mittauksillamme, jotka ottavat huomioon kaikki orientaatiot ja suunnat, vaakasuoraan levyyn kohdistuu yleensä paljon suurempi pystysuora voima kuin kaukana vaakatasosta olevaan levyyn (kuva 2, vasemmalla). Tämän seurauksena vaakasuoran levyn approksimaatio ei enää päde, ja klassiset terramekaaniset mallit ennustavat nostovoiman huomattavasti liian suureksi ja vajoamisen liian pieneksi.
Seuraavat julkaisut:
- Li C, Zhang T, Goldman DI (2013). A terradynamics of legged locomotion on granular media, Science, 339, 1408-1412 (Featured in Science Perspective) PDF
- Ding, Y, Li C, Goldman DI (2013). Swimming in the desert, Physics Today, 66, 68-69 (Invited Paper) PDF
- Maladen RD, Ding Y, Li C, Goldman DI (2009). Undulatory swimming in sand: subsurface locomotion of the sandfish lizard, Science, 325, 314-318 (Featured in Nature News & Views) PDF