Valon heijastuessa tai siirtyessä materiaalirakenteesta tapahtuu polarisaation muutos. Ellipsometria mittaa tätä vastetta, joka riippuu optisista ominaisuuksista ja yksittäisten materiaalien paksuudesta. Ellipsometriaa käytetään ensisijaisesti optisten vakioiden ja kalvon paksuuden määrittämiseen, mutta myös koostumuksen, kiteisyyden, karheuden, seostuskonsentraation ja muiden optisen vasteen muutokseen liittyvien materiaaliominaisuuksien luonnehtimiseen.

Sovellusalueita ovat fysikaalisten tieteiden perustutkimus, puolijohde- ja datanvarastointiratkaisut, litteät näyttöpaneelit, tietoliikennetekniikka, bioanturit ja optiset pinnoitteet. Ellipsometrialla voidaan myös joustavasti mitata useimpia materiaalityyppejä: dielektrisiä aineita, puolijohteita, metalleja, suprajohteita, orgaanisia aineita, biologisia pinnoitteita ja komposiitteja.

Polaroidun valon määritelmä

Valoa voidaan kuvata sähkömagneettisena aaltona, joka kulkee avaruuden läpi. Sitä, miten sähkömagneettisen aallon kenttä käyttäytyy suhteessa tilaan ja aikaan, kutsutaan polarisaatioksi. Valon katsotaan olevan polarisoitumatonta, kun sen suunta ja vaihe ovat täysin mielivaltaisia. Ellipsometria mittaa kuitenkin polarisoitunutta valoa – sähkökenttää, joka kulkee tiettyä reittiä ja jolla on selkeä muoto missä tahansa pisteessä. Sähkömagneettista aaltoa, joka kulkee z-suunnassa, voidaan kuvata sen x- ja y-komponenteilla, koska sen sähkökenttä on aina kohtisuorassa etenemissuuntaan nähden. Kun kaksi ortogonaalista valoaaltoa on samassa vaiheessa, syntyvä valo on lineaarisesti polarisoitunutta. Sen suunta määräytyy suhteellisten amplitudien perusteella. Valoa pidetään ympyräpolarisoituneena, jos ortogonaaliset aallot ovat 90° pois vaiheesta ja niillä on sama amplitudi. Yleisin polarisaatio on elliptinen, ja siinä yhdistyvät ortogonaaliset aallot, joiden amplitudi ja vaihe ovat mielivaltaisia. Ellipsometria on saanut nimensä tästä.

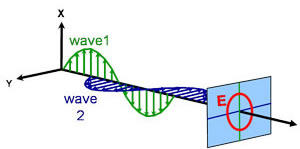
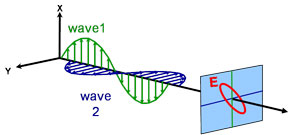
Erilaisia polarisaatiotyyppejä:

Lineaarinen

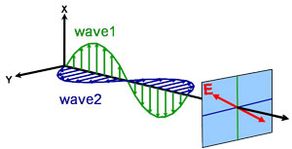
Ympyränmuotoinen

Elliptinen

Optiset ominaisuudet

Optisia ominaisuuksia

Optisia ominaisuuksia, jotka määrittelevät valon vuorovaikutuksen materiaalin kanssa, kuvataan kahdella arvolla. Ne esitetään yleensä kompleksilukuna. Kompleksinen taitekerroin (ñ) koostuu indeksistä (n) ja ekstinktiokertoimesta (k):

Optiset ominaisuudet voidaan kuvata myös kompleksisena dielektrisenä funktiona:

seuraavalla konventioiden välisellä suhteella:

Indeksi kuvaa valon vaihenopeutta kulkiessaan materiaalissa verrattuna valon nopeuteen kulkiessaan tyhjiössä, c:

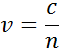
Tullessaan materiaaliin, jonka indeksi on suurempi, valo hidastuu. Koska valoaaltojen taajuus ei muutu, aallonpituus lyhenee. Aaltoenergian häviämistä materiaaliin kuvaa sammumiskerroin, joka liittyy absorptiokertoimeen seuraavasti:

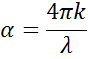
Beerin lain mukaan valo menettää intensiteettiä absorboivassa materiaalissa. Sammumiskerroin osoittaa, kuinka nopeasti valo häviää materiaalissa.

Kuvassa 4 on esitetty valoaalto, joka kulkee kahden eri ominaisuuksiltaan erilaisen materiaalin läpi, ennen kuin se palaa takaisin ympäristöön.

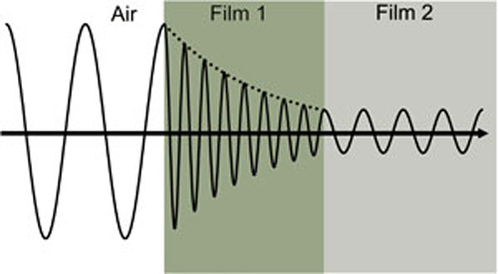
Kuva 4: Valoaalto kulkee ilmasta absorboivaan kalvoon 1 ja sen jälkeen läpikuultavaan kalvoon 2. Vaihenopeus ja aallonpituus muuttuvat molemmissa materiaaleissa taitekertoimen mukaan (Film 1: n=4, Film 2: n=2).

Aallonpituus määrittää optiset vakiot. Kuvassa 5 esitetään TiO2:n optiset vakiot UV:stä IR:ään. Erilaisten valoaallosta energiaa imevien prosessien vuoksi absorptiota (k>0) tapahtuu sekä UV- että IR-aalloissa. IR-absorptio johtuu yleensä molekyylien tai fononien värähtelystä tai vapaista kantajista. UV-absorptio tapahtuu yleensä elektronisten siirtymien vuoksi, joissa valoenergia herättää elektroneja kohonneisiin tiloihin. Kuva 5 osoittaa, että hypoteettiset tai todelliset optiset vakiot eivät ole riippumattomia, vaan ne ovat matemaattisesti yhteydessä toisiinsa Kramers-Kronigin suhteiden kautta.

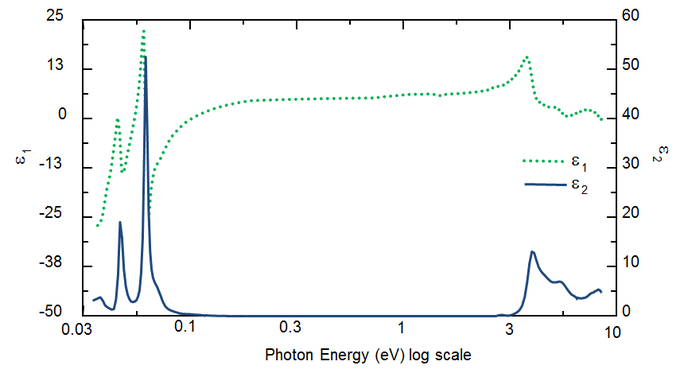
Kuva 5: TiO2-kalvon kompleksinen dielektrinen funktio aallonpituuksilla IR:stä (pieni eV) UV:hen (suuri eV).

Valon ja materiaalien välinen vuorovaikutus

Aina, kun valo vuorovaikuttaa materiaalin kanssa, tämä johtaa raja-arvojen syntymiseen rajapinnassa. Tämän aikana Maxwellin yhtälöiden on aina pysyttävä tyydytettyinä. Alla olevassa kuvassa näkyy, miten osuva valo heijastuu ja taittuu rajapinnassa. Sattuvan säteen ja näytteen normaalin välinen kulma (θi) on yhtä suuri kuin heijastumiskulma (θr). Materiaaliin tunkeutuva valo taittuu kulmassa θt, joka saadaan:

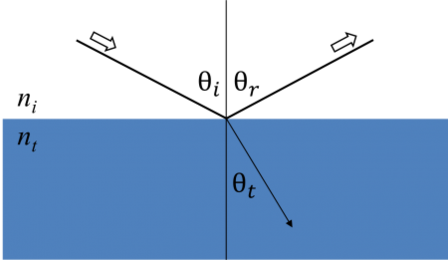
Kuva 6: Valo heijastuu ja taittuu Snellin lain mukaisesti.

Kussakin rajapinnassa osa valosta heijastuu, kun taas loppuosa läpäisee valon taittumiskulmassa. Reunaehdoista riippuen sovelletaan erilaisia ratkaisuja näytteen pinnan suuntaisille ja kohtisuorille sähkökentille. Valo voidaan näin ollen jakaa kohtisuoriin komponentteihin osumistasoon nähden (p- ja s-polarisoitu). Molemmat komponentit voidaan laskea erikseen. Näin Fresnel kuvasi materiaalien välisellä rajapinnalla heijastuvan ja läpäisevän valon määrää:

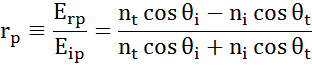
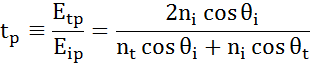
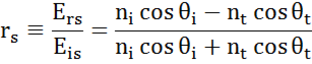
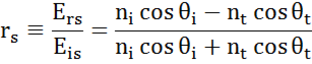
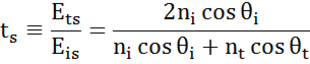
monikerroksisia rajapintoja, joilla on oikeat Fresnelin heijastumis- ja läpäisykertoimet, esiintyy ohuiden kalvojen ja monikerrosrakenteissa. Jotta heijastunut tai läpäisty säde voidaan määritellä oikein, kunkin valokomponentin suhteellista vaihetta on seurattava. Kalvon vaihepaksuus määritetään siis seuraavasti:

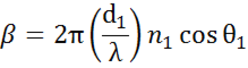
Kun useat valoaallot asettuvat päällekkäin, syntyy interferenssiä, joka riippuu kunkin yksittäisen valoaallon suhteellisesta vaiheesta. Alla olevassa kuvassa on esitetty heijastuneen säteen valoaaltojen yhdistyminen ja niitä vastaavat Fresnel-laskelmat.

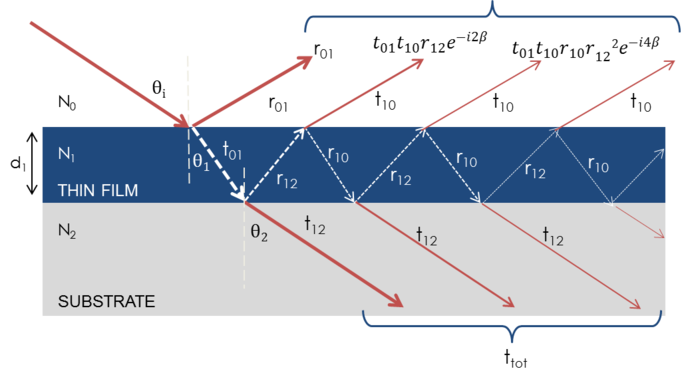
Kuva 7: Valo heijastuu ja taittuu jokaisessa yksittäisessä rajapinnassa, mikä johtaa useisiin sädekehiin ohuessa kalvossa. Säteiden interferenssi riippuu sähkökenttien suhteellisesta vaiheesta ja amplitudista. Säteen reaktio voidaan laskea Fresnelin heijastus- ja läpäisykertoimien avulla.

Mittaukset

Ellipsometria mittaa pääasiassa sitä, miten p- ja s-komponentit reagoivat toisiinsa nähden heijastuksen tai läpäisyn aikana. Referenssisäde on siis aina osa koetta. Tunnettu polarisaatio heijastetaan tai lähetetään näytteestä ja mitataan lähtöpolarisaatio. Polarisaation muutos on ellipsometriamittaus:

Kuvassa 6 on esitetty tyypillinen näytteen ellipsometriamittaus. Lineaarisesti osuvassa valossa on sekä p- että s-komponentteja. Heijastuneessa valossa näkyy sekä p- että s-polarisoidun valon amplitudi- ja vaihemuutokset. Nämä muutokset mitataan ellipsometrialla.

Ellipsometriatietojen keräämiseen tarvitaan: valonlähde, polarisaatiogeneraattori, näyte, polarisaatioanalysaattori ja ilmaisin. Sekä polarisaatiogeneraattori että analysaattori koostuvat optisista osista, jotka manipuloivat polarisaatiota: kompensaattorit, polarisaattorit ja vaihemodulaattorit. Tyypilliset ellipsometrikokoonpanot sisältävät pyörivän analysaattorin (RAE), pyörivän polarisaattorin (RPE), pyörivän kompensaattorin (RCE) ja vaihemodulaattorin (PME). Alla olevassa kuvassa on esitetty RAE-kokoonpano.

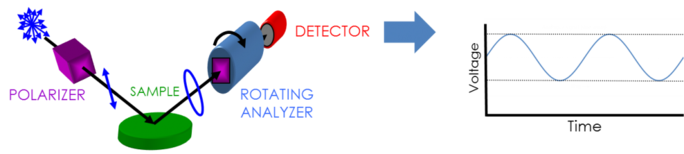
Valonlähteestä tuotetaan polarisoimatonta valoa, joka lähetetään polarisaattorin läpi. Polarisaattori asetetaan siten, että vain tietyn sähkökentän suuntainen valo pääsee läpi. Koska polarisaattorin akseli on kohdistettu p- ja s-tasojen väliin, molemmat pääsevät näytteen pinnalle. Nyt lineaarisesti polarisoitunut valo heijastuu näytteen pinnasta, jolloin siitä tulee elliptisesti polarisoitunutta, ja lähetetään sitten jatkuvasti pyörivän polarisaattorin (”analysaattori”) läpi. Läpi kulkevan valon määrä riippuu polarisaattorin suunnasta suhteessa näytteen sähkökentän ellipsiin. Heijastuneen polarisaation määrittämiseksi valo muunnetaan ilmaisimessa elektroniseksi signaaliksi. Vertaamalla tätä dataa määritettyyn tulopolarisaatioon saadaan tietoa näytteen heijastuksen aiheuttamasta muutoksesta: Psi:n ja Delta:n ellipsometrinen mittaus.

Data-analyysi

Ellipsometriaa käytetään materiaalikalvon paksuuden tai optisten vakioiden määrittämiseen mittaamalla valon polarisaation muutoksia. ”Pseudo” optiset vakiot ellipsometriamittauksesta voidaan johtaa kääntämällä yksittäiselle heijastukselle määritetyt tiedot päinvastaisiksi. Tämä on hyödyllistä bulkkimateriaalille.

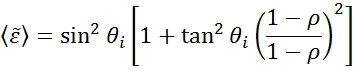
Yllä olevaa yhtälöä ei lasketa pintakerroksilla. Bulkkimateriaaleissa on kuitenkin yleensä pintaoksidia tai karheutta. Suora inversio sisältää nämä tiedot osana bulkin optisia vakioita. Kuvassa 10 on yleiskatsaus ellipsometriamittauksissa käytettävästä tyypillisestä data-analyysiprosessista. Koska tarkkaa yhtälöä ei voida kirjoittaa, tarvitaan regressioanalyysi. Vastaus on usein ylimääritetty vain muutamalla tuntemattomalla ja sadoilla kokeellisilla datapisteillä. Regressioanalyysin avulla kaikki mitatut tiedot voidaan ottaa huomioon ratkaisua määritettäessä.

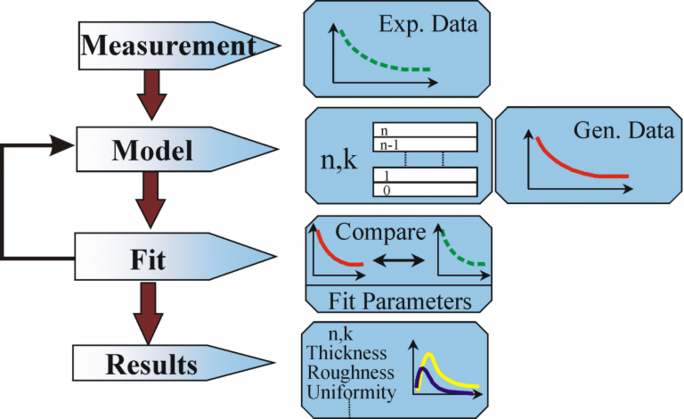
Kuva 10: Ellipsometrian data-analyysin vuokaavio.

Data-analyysissä käytetään seuraavaa menettelyä: Näyte mitataan ja näytteestä tehdään malli. Tämän mallin avulla lasketaan oletetut tulokset Fresnelin yhtälöistä, jotka kuvaavat kunkin materiaalin paksuutta ja optisia vakioita. Jos nämä arvot eivät ole tiedossa, tehdään alustavan laskennan arviointi. Laskettuja arvoja verrataan kokeellisiin tietoihin. Jotta kokeelliset ja laskentatiedot vastaisivat paremmin toisiaan, tuntemattomia materiaalitietoja voidaan muuttaa. Kokeellisten tietojen pisteiden pitäisi kuitenkin aina olla enemmän kuin tuntemattomien parametrien. Esimerkiksi yhden aallonpituuden ellipsometrillä voidaan määrittää enintään kaksi materiaaliominaisuutta, koska se tuottaa täsmälleen kaksi datapistettä: Ψ, Δ (Psi ja Delta). Regressiota käytetään mallin ja kokeen parhaan yhteensopivuuden löytämiseksi. Tietokäyrien välinen ero kvantifioidaan estimaattorin, kuten MSE:n (Mean Squared Error) avulla. Tuntemattomia ominaisuuksia vaihdellaan, kunnes saavutetaan pienin MSE. Tämä tarkoittaa, että pienin MSE vastaa parasta vastausta.

Katso alla olevasta kuvasta MSE-käyrä kalvon paksuuden funktiona läpinäkyvälle kalvolle piillä. Pienin MSE-arvo esiintyy 749 nm:n paksuudella huolimatta useista paikallisista minimeistä. Näin ollen oikea kalvon paksuus on myös 749 nm. Regressioalgoritmi saattaa pitää paikallista minimiä oikeana. Oikean paikallisen minimin määrittämiseksi on siis viisasta verrata tuloksia silmämääräisesti pienimmän MSE:n löytämiseksi.

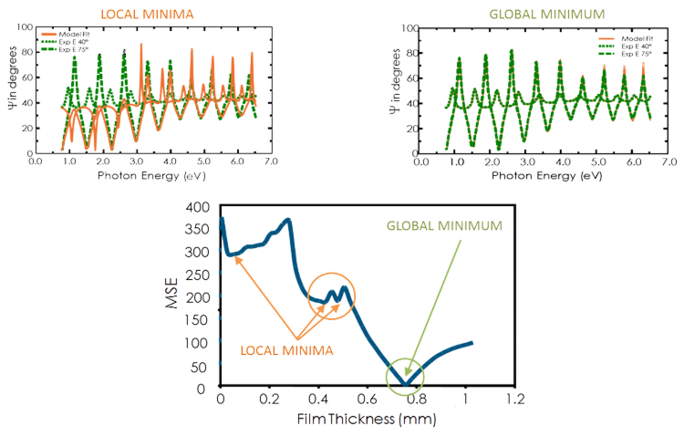
Kuva 11, ylhäällä oikealla: Kokeelliset tiedot ja vastaavat käyrät, jotka on luotu mallille globaalissa minimissä. Kuva 11, ylävasemmalla: Vastaava käyrä paikallisessa minimissä lähellä 0,45 µm:n paksuutta voidaan helposti tunnistaa virheelliseksi tulokseksi. Kuva 11, alhaalla: MSE-käyrä paksuuden suhteen osoittaa globaalin minimin. Regressioalgoritmi voi antaa paikalliset minimit, mutta ei lopullista tulosta.

Kalvon paksuuden määrittäminen

Kalvon paksuus määritetään yleensä pinnasta heijastuvan valon ja kalvon läpi kulkevan valon interferenssin avulla. Se, pidetäänkö tätä interferenssiä rakentavana vai tuhoavana, riippuu pintaheijastukseen yhtyvän valon suhteellisesta vaiheesta. Interferenssi sisältää sekä amplitudi- että vaiheinformaatiota. Δ:stä saatava vaiheinformaatio on hyvin herkkä kalvoille, joiden paksuus on jopa alle monokerroksen. Alla olevassa kuvassa on vertailu heijastuneen intensiteetin ja ellipsometrian välillä samassa sarjassa ohuita SiO2-kerroksia Si:llä. Kunkin kalvon heijastuvuus on lähes sama, kun taas Δ:ssä on suuria vaihteluita.

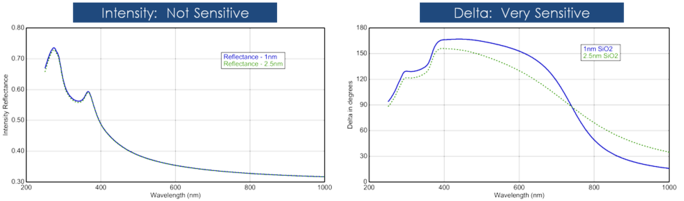
Kuva 12, vasen: Heijastunut intensiteetti ja ellipsometrinen delta (oikealla) kahdelle ohuelle oksidille piillä. Intensiteettimittaus ei osoita, että delta on erittäin herkkä nanometrin kokoisille kalvoille.

Ellipsometriaa käytetään yleisesti kalvoille, joiden paksuus on alle nanometristä muutamaan mikrometriin. Useita kymmeniä mikrometrejä paksummilla kalvoilla interferenssivärähtelyjä voidaan ratkaista vain yhä vaikeammin, paitsi jos käytetään pidempiä infrapuna-aallonpituuksia. Tämän vuoksi paksummille kalvoille käytetään yleensä muita mittaustekniikoita.

Paksuuden mittaamiseksi osan valosta on kuljettava koko kalvon läpi ja palattava sitten takaisin pinnalle. Valoa absorboivilla materiaaleilla optisia paksuusmittauksia voidaan tehdä vain ohuille ja puoliksi läpinäkymättömille kerroksille, ellei niitä tehdä spektrialueilla, joilla absorptio on vähäisempää. Esimerkiksi orgaaninen kalvo, joka absorboi UV- ja IR-valoa, voi olla läpinäkyvä keskinäkyvillä aallonpituuksilla. Metallit absorboivat voimakkaasti kaikilla aallonpituuksilla, joten suurin määritettävissä oleva kerroksen paksuus on noin 100 nm.

Optiset vakiot

Optisilla vakioilla on tärkeä merkitys paksuusmittauksissa. Kalvon paksuus vaikuttaa kalvon läpi kulkevan valon kulkupituuteen, indeksi määrittää valoaallon nopeuden ja taitekulman. Molemmat vaikuttavat siis kalvon läpi kulkevan valon ja pintaheijastuksen väliseen viiveeseen. On tarpeen määrittää n ja k sekä paksuus, jotta optisesta mittauksesta saadaan oikeat tulokset.

Koska materiaalin optiset vakiot vaihtelevat eri aallonpituuksille, kaikki ellipsometrillä analysoitavat aallonpituudet on määritettävä erikseen. Materiaalin vaste kullakin aallonpituudella voidaan ennakoida käyttämällä optisten vakioiden taulukkoa. Jotta vältyttäisiin tuntemattomien optisten vakioiden vaivalloiselta säätämiseltä aallonpituuskohtaisesti, on suotavaa käyttää kaikkia aallonpituuksia samanaikaisesti. Esimerkiksi dispersiosuhteen säädettävien parametrien avulla optisen vakion kokonaismuoto saadaan vastaamaan kokeellisia tuloksia. Verrattuna yksittäisten n- ja k-arvojen säätämiseen jokaiselle aallonpituudelle, tuntemattomien vapaiden parametrien määrä vähenee huomattavasti.

Cauchyn tai Sellmeierin suhteita käytetään usein kuvaamaan indeksiä läpinäkyville materiaaleille, jolloin Cauchyn suhde on tavallisesti:

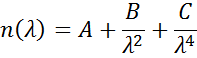
ja kolme termiä sovitetaan siten, että ne täsmäävät materiaalin taitekerroinlukuihin. Cauchyn suhdetta ei rajoita Kramers-Kronigin (KK) johdonmukaisuus ja se voi johtaa epäfysikaaliseen dispersioon. Toisaalta Sellmeierin relaatio edellyttää Kramers-Kronigin (KK) johdonmukaisuutta, jolla varmistetaan, että optinen dispersio säilyttää realistisen muodon. Sellmeierin relaatio kirjoitetaan tyypillisesti seuraavasti:

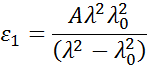
Aabsorboivilla materiaaleilla on usein läpinäkyvä aallonpituusalue, joka voidaan mallintaa Cauchyn tai Sellmeierin relaatiolla. Kun taas absorboivalla alueella on kuitenkin otettava huomioon sekä reaaliset että imaginaariset optiset vakiot. Eri materiaalien absorption kuvaamiseksi monet dispersiosuhteet hyödyntävät oskillaattoriteoriaa, mukaan lukien Lorentz, Harmonic ja Gauss. Kaikilla niillä on samankaltaisia ominaisuuksia, joissa absorptio-ominaisuuksia kuvataan amplitudilla, levenemisellä ja keskipisteen energialla (joka liittyy valon taajuuteen). Reaalikomponentin muoto lasketaan Kramers-Kronigin johdonmukaisuuden avulla sen jälkeen, kun imaginaarinen käyttäytyminen on kuvattu oskillaattorilla. Mitatun spektrialueen ulkopuolella tapahtuvan mahdollisen lisäabsorption huomioon ottamiseksi reaalikomponenttiin lisätään offset. Lorentz-oskillaattori voidaan kirjoittaa seuraavasti:

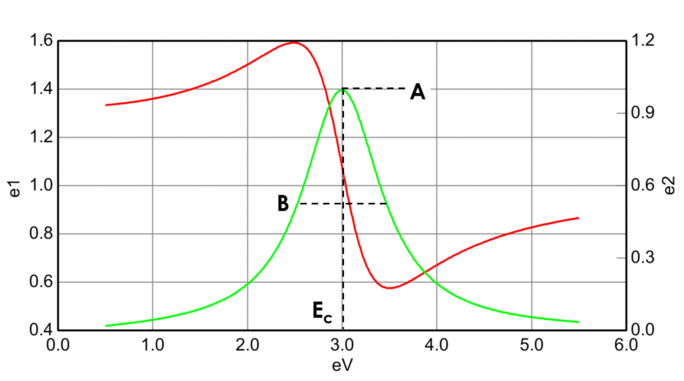
Kuvassa 13 esitetään myös tyypillisen Lorentz-oskillaattorin amplitudi (A), leveneminen (B), keskienergia (Ec) ja offset (e1, off set). Energia E liittyy aallon taajuuteen n:

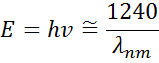
Planckin vakio h ja aallonpituus λ annetaan nanometreinä. Muut dispersiomallit, kuten Tauc-Lorentz ja Cody-Lorentz, sisältävät termejä, jotka kuvaavat kaistaläpän energiaa.

Lisälukemista

Ellipsometria on vakiintunut optinen tekniikka ohuiden kalvojen ja bulkkimateriaalien mittaamiseen. Se käyttää materiaalirakenteesta tapahtuvan heijastuksen/läpäisyn aiheuttamia polarisaatiomuutoksia materiaalin ominaisuuksien, kuten paksuuden ja optisten vakioiden, määrittämiseen.

Aspnes D.E. (1985). The Accurate Determination of Optical Properties by Ellipsometry. In: Palik E.D. (toim.) Handbook of Optical Constants of Solids, s. 89-112. Academic Press, Orlando.

Azzam R.M.A. ja Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, Alankomaat.

Boccara A.C., Pickering C. ja Rivory J. (toim.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E. ja Irene E.A. (toim.), (1998). ”Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd.,

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications. 2007

Gottesfeld S., Kim Y.T. ja Redondo A. (1995). ”Ellipsometrian ja spektroellipsometrian viimeaikaiset sovellukset sähkökemiallisissa järjestelmissä”, In: I. Rubinstein (toim.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, s. 425-479. Academic Press, San Diego, Kalifornia.

Johs B. et al (1999). ”Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, s. 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). ”Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (toim.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. ja Richter W. (1996). ”Spectroscopic Ellipsometry” in: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. ja McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. ja Irene E.A. (toim.), 2005, Handbook of Ellipsometry (Ellipsometrian käsikirja), William Andrew Publishing, New York.

Tompkins, H. G. ja Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. ja Snyder P.G. (1992). ”Variable Angle Spectroscopic Ellipsometry” in: Brundle CR, Evans CA ja Wilson S (toim.) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). ”Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, s. 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). ”Ellipsometry, Variable Angle Spectroscopic” in: Webster J.G. (toim.) Wiley Encyclopedia of Electrical and Electronics Engineering, s. 109-116. John Wiley & Sons, New York.

.