Mikä on kaltevuuden leikkausmuoto

Kaltevuuden leikkausmuoto on yksi kolmesta muodosta, joilla voimme ilmaista suoran. Muita muotoja kutsutaan pisteen kaltevuusmuodoksi ja vakiomuodoksi, mutta käytämme tässä osiossa enimmäkseen kaltevuuden leikkausmuotoa. Käyttämällä slope intercept -muotoa ilmaisemme suoran yhtälön seuraavasti:

y=mx+by = mx + by=mx+b

Tiedät ehkä xxx:n ja yyy:n olevan kuvaajan pisteen koordinaatteja, mutta mitkä ovat mmm ja bbb?

Mitä on b yhtälössä y=mx+b?

Kirjain b on luku, joka kuvaa sitä, milloin suora sivuaa y-akselia. Kutsumme tätä myös nimellä ”y-katkoviiva”. Missä tämä paikka on? Se olisi numero 3, koska siinä kohtaa y-akseli ja suora leikkaavat toisensa. Tämä tarkoittaa, että voimme päätellä, että b = 3.

Mikä on m kaltevuuden leikkausmuodossa?

Kirjain m on luku, joka kuvaa suoran kaltevuutta. Jotkut kutsuvat kaltevuutta nousuksi yli juoksun. Muistetaan, että jos meillä on kaksi pistettä, voimme löytää näiden kahden pisteen kaltevuuden käyttämällä kaltevuuskaavaa

m=riserun=y2-y1x2-x1m = \frac{rise}{run} = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=runrise=x2-x1y2-y1

Sama ajatus toimii myös tässä. Jos otamme kaksi mitä tahansa pistettä suoralle, voimme löytää suoran kaltevuuden yllä olevan kaavan avulla! Käytetään esimerkiksi tätä suoraa.

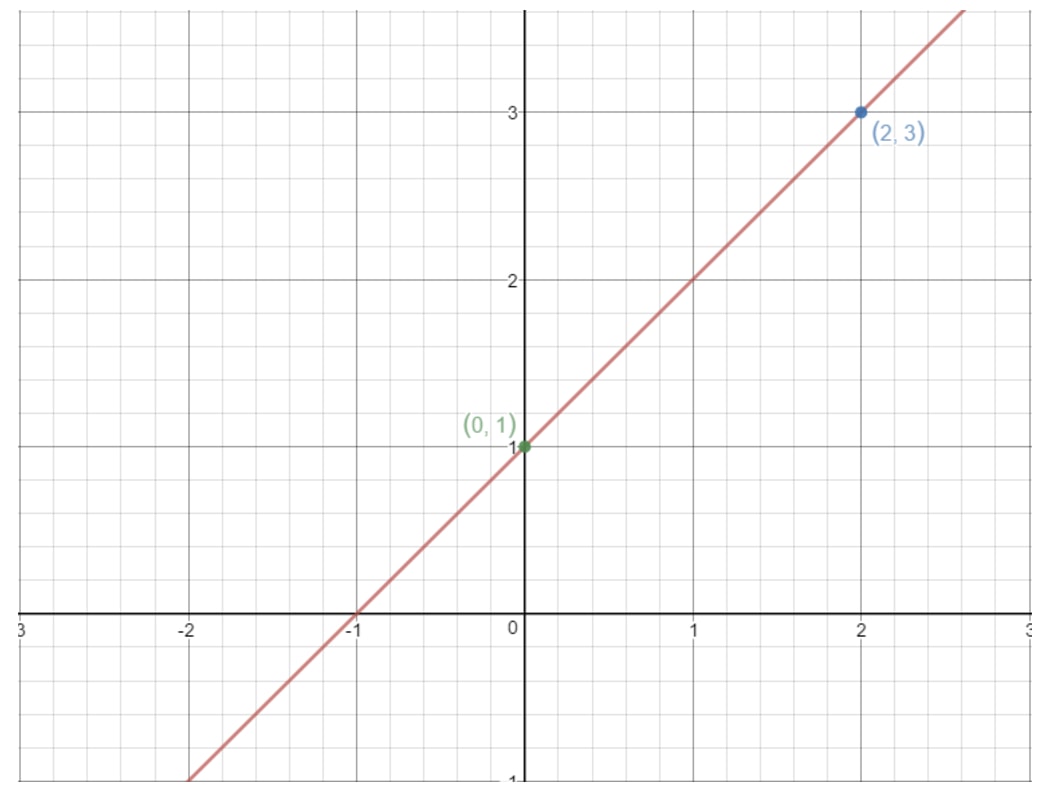
Huomaa, että tässä kuvaajassa ovat pisteet (2, 3) ja (0, 1). Miksi emme siis käytä näitä kahta pistettä löytääksemme suoran kaltevuuden? Kaavan avulla saisimme:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2-2=1= 1=1

Tämä tarkoittaa, että tämän suoran kaltevuus on 111!

Erikoislaatuinen juttu kaltevuuksissa on se, että voimme käyttää mitä tahansa kahta suoran pistettä sen löytämiseen. Jos siis ottaisit kaksi eri pistettä tältä suoralta, saisit silti tulokseksi, että kaltevuus on 111.

Miten kirjoittaa yhtälö kaltevuuden leikkausmuodossa?

Voit ehkä tietää, miltä kaltevuuden leikkausmuoto näyttää, mutta puolet ajasta sinulle annetaan yhtälöitä, jotka eivät ole tässä muodossa. Niinpä sinun tehtäväsi on muuttaa se kaltevuusvälin muotoon. Miten se tehdään? Tavoitteena on aina eristää yyy-termi. Sanotaan esimerkiksi, että sinulle annetaan yhtälö

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

eristää yyy, siirretään 6x+46x + 46x+4 yhtälön oikealle puolelle

2y=-6x-42y = -6x – 42y=-6x-4

Nyt 222 on yyy:n tiellä, joten pääsemme siitä eroon jakamalla yhtälön molemmat puolet luvulla 222.

2y2=-6x-42\frac{2y}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Koska yyy on eristetty, nähdään, että se on kaltevuus-leikkausmuodossa y=mx+by = mx + by=mx+b, missä m=-3m = -3m=-3, ja b=-2b = -2b=-2.

Nyt kun tunnemme y:n leikkauspisteen ja kaltevuuden todella hyvin, niin miksi emme katsoisi erityisiä kysymyksiä niiden löytämisestä!

Miten löydetään y:n leikkauspiste?

Kysymys 1: Käyttämällä lineaarista yhtälöä y=12x+5y = \frac{1}{2} x + 5y=21x+5, löydä y:n leikkauspiste.

Huomaa tässä, että yhtälö on jo valmiiksi kaltevuuden ja leikkauspisteen muodossa y=mx+by = mx + by=mx+b. Meidän on vain selvitettävä, mikä on bbb. Näemme, että b=5b = 5b=5, joten y-poikkileikkaus on 555.

Tehdään hieman vaikeampi kysymys.

Kysymys 2: Määritä y-poikkileikkaus yhtälöstä 2x-4y=82x – 4y = 82x-4y=8

Nyt tämä lineaarinen yhtälö ei ole kaltevuus-poikkileikkaus -muodossa, joten meidän on ensin muutettava se tähän muotoon. Tavoitteenamme on eristää yyy tästä yhtälöstä.

Huomaa, että jos siirrämme 2x2x2x yhtälön oikealle puolelle, saamme:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Ja nyt jakamalla molemmat puolet -4-4-4-4:llä saamme:

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4-4-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Nyt vaihtamalla kahden termin paikkaa saadaan:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Kysymys 3: Määritä 4y-8=04y – 8 = 04y-8=0:n y-leikkaus.

Tämä saattaa näyttää hieman oudolta, koska siinä ei ole xxx-termiä, mutta tavoitteemme pysyy samana. Aiomme eristää yyy:n.

Siirtämällä -8-8-8 yhtälön oikealle puolelle saamme:

4y=84y = 84y=8

Jakamalla yhtälön molemmat puolet 444:llä saamme

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y=2y=2y=2

Nyt tämä ei ehkä näytä siltä, mutta yhtälö on kaltevuuden ja leikkauksen muodossa. On vain niin, että m=0m = 0m=0, joten koko mxmxmxmx-termi on kadonnut. Kirjoitetaan vain yhtälö uudelleen muotoon

y=0m+2y = 0m + 2y=0m+2

Havainnosta voidaan todeta, että b=2b = 2b=2, joten y:n leikkaus on 222. Tehdään vielä yksi kysymys.

Kysymys 4: Määritä (jos mahdollista) yhtälön 5x-15=05x – 15 = 05x-15=0 y-poikkileikkaus.

Tämä on mielenkiintoinen, koska yhtälössä ei ole yyy-termiä. Joten miten meidän pitäisi laittaa se slope intercept -muotoon? No, ainoa asia, jonka voimme nyt tehdä, on eristää xxx, joten kokeillaan sitä toistaiseksi.

Muuttamalla 151515 yhtälön oikealle puolelle saamme:

5x=155x = 155x=15

Jakamalla yhtälön molemmat puolet saadaan:

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Piirretään tämä nyt kuvaajaan. Huomaa, että tässä yhtälössä xxx:n on pakko olla 333 eikä se voi olla mitään muuta. Se ei kuitenkaan sano mitään yyy:stä, joten yyy voi olla mitä tahansa. Jos kirjoittaisimme arvotaulukon, saisimme:

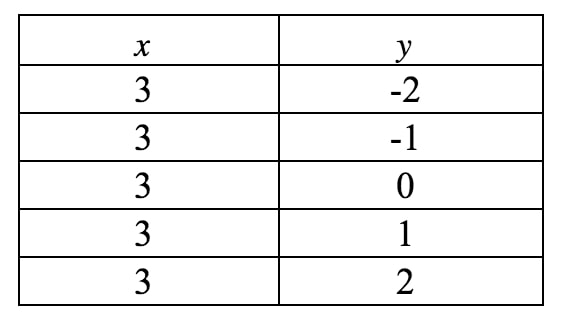
Jos piirtäisimme nämä pisteet koordinaattitasolle ja piirtäisimme viivan, saisimme:

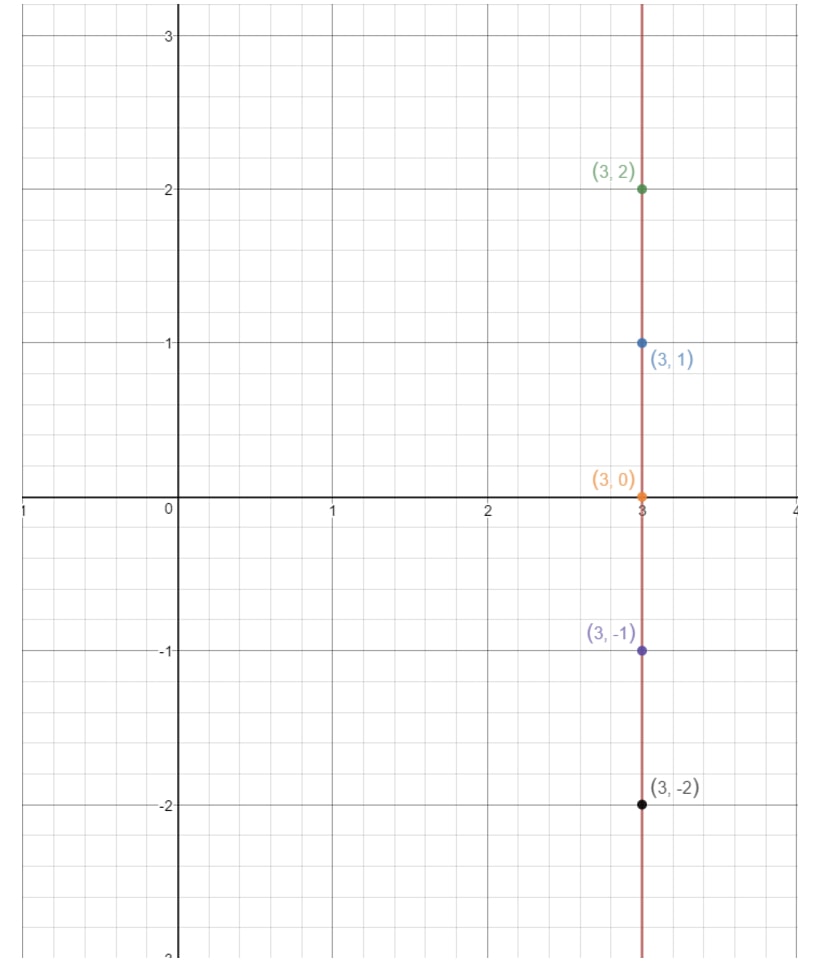
Huomaa, että viiva ei koskaan kosketa y-akselia. Tämä tarkoittaa, että yhtälöllä ei ole y-leikkauspistettä. Nyt kun olemme käsitelleet kaikki y-poikkileikkauksen löytämisen tapaukset, tarkastellaan kysymyksiä, joissa pyydetään löytämään kaltevuus!

Miten löytää yhtälön kaltevuus?

Kysymys 5: Etsi yhtälön y=32x+1y = \frac{3}{2}x + 1y=23x+1 kaltevuus

Kysymys 6: Määritä lineaarisen yhtälön 6x-6y=06x – 6y = 06x-6y=0 kaltevuus

Kuten huomaat, yhtälö ei ole kaltevuuden leikkauspisteen muodossa, joten meidän on ensin muunnettava se tähän muotoon. Tavoitteenamme on eristää yyy.

Siirtämällä 6x6x6x yhtälön oikealle puolelle saadaan:

-6y=-6x-6y = -6x-6y=-6x

Jakamalla molemmat puolet luvulla -6-6-6 saadaan:

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6-6xy=xy = xy=x

Huomaa, että tämä on itse asiassa kaltevuuden leikkausmuodossa y=mx+by = mx + by=mx+b. Kyse on vain siitä, että y:n leikkauspiste bbb on tässä tapauksessa 000, ja xxx on sama kuin 1x1x1x. Voimme siis kirjoittaa yhtälön uudelleen muotoon:

y=1x+0y = 1x + 0y=1x+0

Nyt havainnoimalla näemme, että m=1m = 1m=1. Koska mmm on kaltevuus, niin kaltevuuden on oltava 111. Tehdään hieman vaikeampi

Kysymys 7: Määritä 2y-4=02y – 4 = 02y-4=0

Tämä on taas hieman outo, koska meillä ei ole xxx-termiä. Tavoitteenamme on kuitenkin edelleen eristää yyy.

Siirtämällä -4-4-4 yhtälön oikealle puolelle saamme:

2y=42y = 42y=4

Jakamalla yhtälön molemmat puolet 222:lla saadaan:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Tässä nähdään, että se on nyt kaltevuuden leikkausmuodossa, paitsi että termi mxmxmx on piilossa, koska m=0m = 0m=0. Voimme siis kirjoittaa yhtälömme uudelleen seuraavasti:

y=0x+2y = 0x + 2y=0x+2

Koska m=0m = 0m=0, niin meillä on nollakaltevuus. Jos mietit, miltä näyttää viiva, jolla on 000 kaltevuus, niin tässä on kuvaaja, jonka voit katsoa.

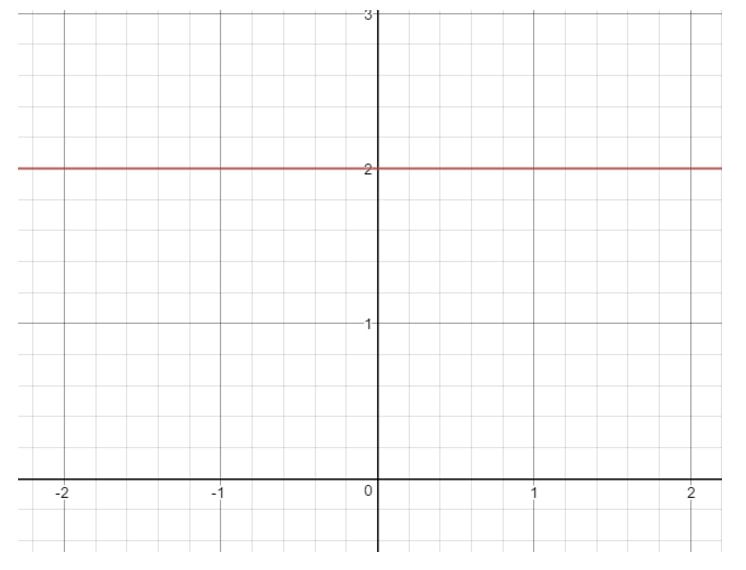
Kysymys 8: Etsi (jos mahdollista) lineaarisen yhtälön 16-4x=016 – 4x = 016-4x=0

Tässä tapauksessa yyy:tä ei voida eristää, koska yyy-termiä ei ole. Joten ainoa mitä voimme tehdä on eristää xxx.

Siirtämällä 161616 yhtälön oikealle puolelle saadaan:

-4x=-16-4x = -16-4x=-16

Jakamalla molemmat puolet luvulla -4-4-4 saamme:

-4x-4=-16-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4-4x=-4-16x=4x = 4x=4

Tämä ei edelleenkään ole kaltevuuden leikkausmuodossa, joten ainoa toivomme kaltevuuden saamiseksi on piirtää tästä suorasta kuvaaja. Jälleen näemme, että xxx on aina pakko olla 444, mutta yyy voi olla mitä tahansa, koska yyy-termiä ei ole. Jos kirjoittaisimme arvotaulukon, saisimme:

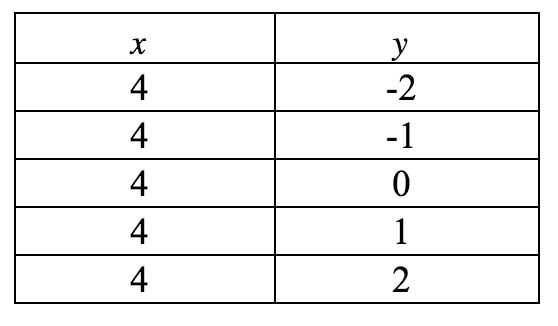
Jos piirrämme nämä pisteet koordinaattitasolle ja piirrämme suoran, saamme:

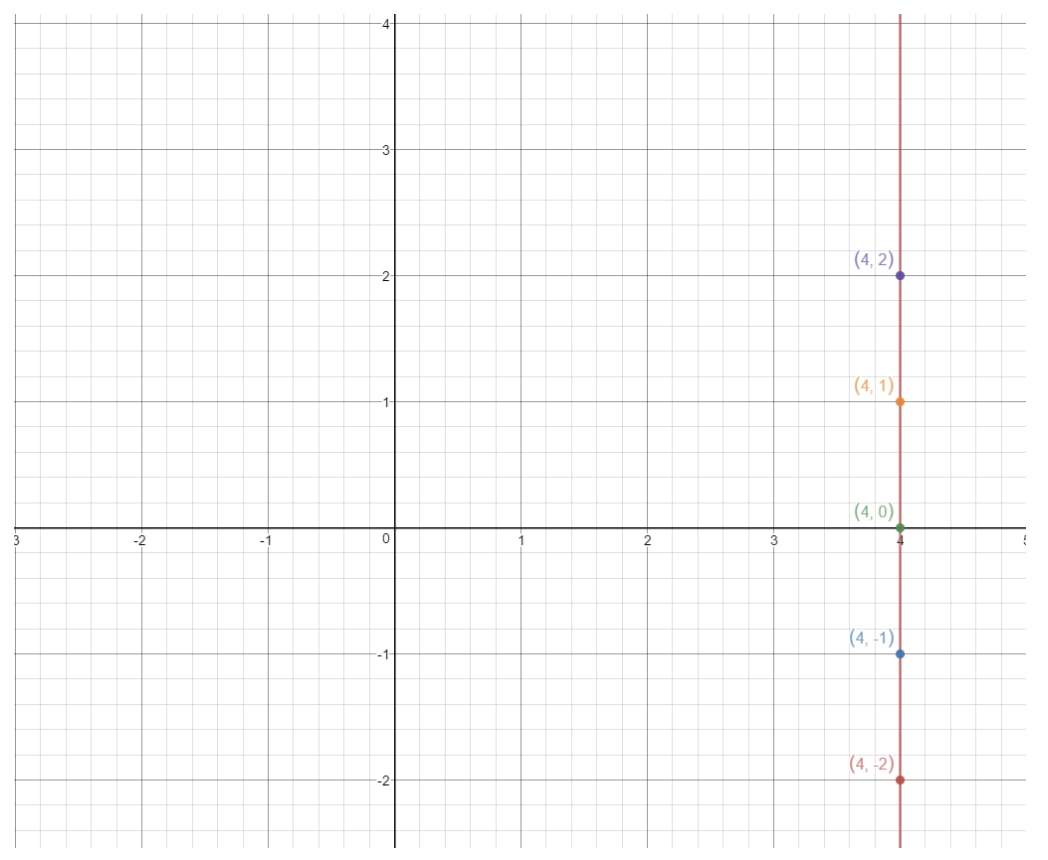
Tämä on pystysuora viiva. Mikä on siis pystysuoran viivan kaltevuus? Yritetään selvittää se selvittämällä nousu ja juoksu. Katso, kuinka tämä viiva nousee aina äärettömästi, mutta juoksua ei ole lainkaan. Se tarkoittaa siis, että nousu on 000. Jos siis laskemme kaltevuuden, niin saamme:

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

Me emme voi jakaa 000:lla, joten meillä on itse asiassa määrittelemätön kaltevuus.

Mikä on määrittelemätön kaltevuus?

Määrittelemätön kaltevuus on kaltevuus, joka menee kuvaajassa suoraan ylöspäin. Kuten yllä olevassa kuvaajassa nähdään, kaltevuus nousee äärettömästi eikä sillä ole juoksua. Tämän seurauksena saamme määrittelemättömän kaltevuuden, koska emme voi jakaa 000:lla.

Yleisesti saamme aina määrittelemättömän kaltevuuden aina, kun saamme suoran pystysuoran viivan!

Katsotaanpa vielä muutamia muita uniikkeja kysymyksiä!

Yhtälön löytäminen yhdestä pisteestä

Kysymys 9: Pisteen (2, 6) kautta kulkee yhtälöyhtälön y=-5x+by = -5x + by=-5x+b. Etsi ”bbb”.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Isoleoimalla ja ratkaisemalla bbb saadaan:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Muistakaamme, että bbb:tä kutsutaan myös nimellä y-ylänpätkä, joten y-ylänpätkä on myös 161616!

Kaltevuuden löytäminen kahdesta pisteestä

Kysymys 10: Kun on annettu kaksi pistettä (6, 1) ja (-10, 9), etsitään suoran kaltevuus.

Palautetaan mieleen, että kun halutaan löytää suoran kaltevuus, käytetään kaltevuusyhtälöä

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Siten tätä kaavaa käyttämällä saadaan:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

Mitä, jos sen sijaan meidän on tarkoitus löytää koko suoran yhtälö?

Suoran yhtälö annettuna kahdelle pisteelle

Kysymys 11: Kun on annettu kaksi pistettä (-6, 1) ja (2, 6), löydetään kaltevuuden leikkausmuotoinen yhtälö.

Yritämme periaatteessa löytää yhtälön muodossa y=mx+by = mx + by=mx+b. Tätä varten meidän on etsittävä mmm ja bbb.

Muistetaan, että mmm:n löytämiseksi käytämme kaltevuusyhtälöä

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Siten tätä kaavaa käyttämällä saadaan:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Siten meillä on nyt yhtälö

y=58x+by = \frac{5}{8}x + by=85x+b

Jatkossa meidän on etsittävä bbb. Ratkaistaksemme bbb, valitsemme jommankumman annetuista pisteistä ja liitämme sen yhtälöön. Voimme tehdä sen, koska molemmat pisteet sijaitsevat suoralla, ja kaikki suoralla olevat pisteet täyttäisivät yhtälön. Käytetään pistettä (2, 6). Nähdään, että:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

eristämällä bbb saadaan:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Sijoittamalla tämä desimaalimuodossa saadaan, että b=4.75b = 4.75b=4.75. Näin ollen kaltevuuden leikkausmuotoinen yhtälömme on:

y=58x+4.75y = \frac{5}{8}x + 4.75y=85x+4.75

Viimeinen asia, jota käsittelemme tässä osiossa, on suoran toimialueen ja vaihteluvälin löytäminen.

Kuinka löydetään toimialue ja vaihteluväli?

Suoran toimialueen selvittämiseksi kysymme itseltämme pohjimmiltaan seuraavanlaisen kysymyksen: Mikä voi olla xxx? Jos xxx voi olla näitä arvoja, niin lisäämme ne toimialueeseen.

Sama pätee myös alueeseen. Mitä yyy voi olla? Jos yyy voi olla näitä arvoja, lisäämme ne alueeseen. Tehdään esimerkki.

Kysymys 12: Etsi yhtälön y=2x+1y = 2x + 1y=2x+1 toimialue ja vaihteluväli.

Huomaa, että jos piirrämme tämän suoran kuvaajan, niin saamme:

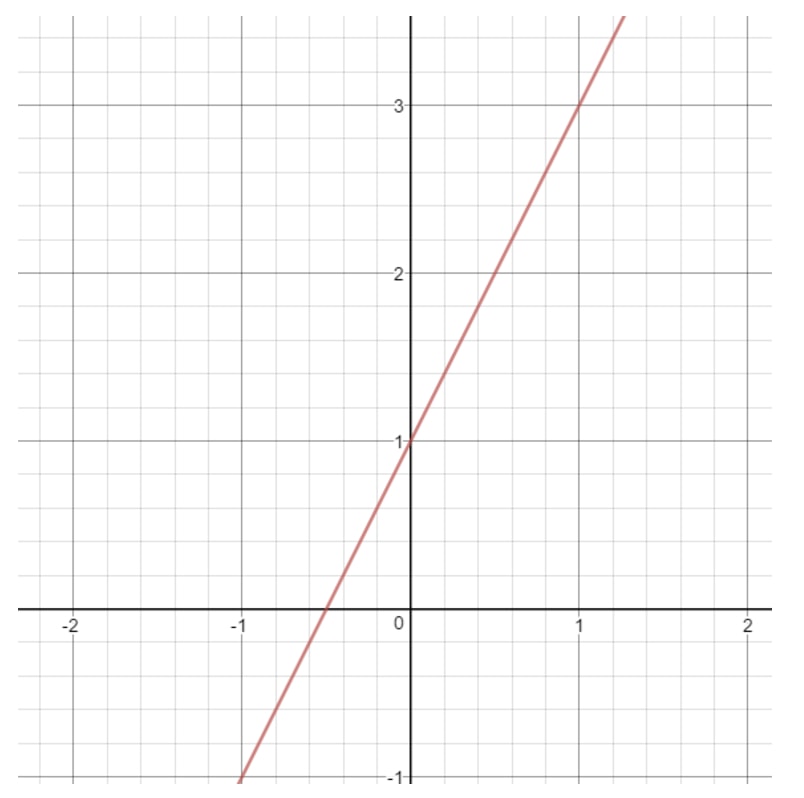
Mitä xxx voi olla tällä suoralla? Huomaa, että xxx voi olla mitä tahansa, koska millä tahansa xxx:n arvolla saamme pisteen, joka on suoralla. Sama koskee y:tä. Voimme aina valita yyy-arvon, joka antaa meille pisteen suoralla. Sanomme siis, että

Domain: {x∈\in∈R}Range: {y∈\in∈R}

jossa R tarkoittaa ”kaikkia reaalilukuja”. Tehdään vaikeampi kysymys.

Kysymys 13: Etsi yhtälön y=-2y = -2y=-2 toimialue ja alue.

Jos nyt piirretään tämä suora kuvaajaan, saadaan:

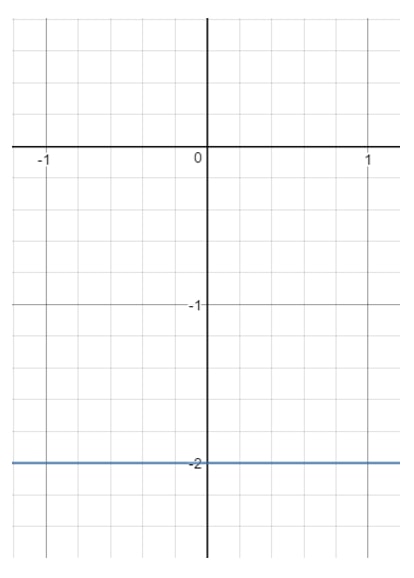
Huomaa, että xxx voi olla mikä tahansa, koska millä tahansa xxx:n arvolla saamme pisteen, joka on suoralla niin kauan kuin y=-2y = -2y=-2. Katsotaan kuitenkin yyy. Näet, että yyy on pakotettu -2-2-2-2 eikä se voi olla mitään muuta. Heti kun valitaan jokin muu yyy:n arvo (kuten 111), kyseinen piste on suoran ulkopuolella. Tämä tarkoittaa siis seuraavaa:

Domain: {x ∈\in∈ R}Range: {y = -2}

Kysymys 14: Etsi yhtälön x=1x = 1x=1 toimialue ja alue.

Jos nyt piirretään tämä viiva kuvaajaan, saadaan:

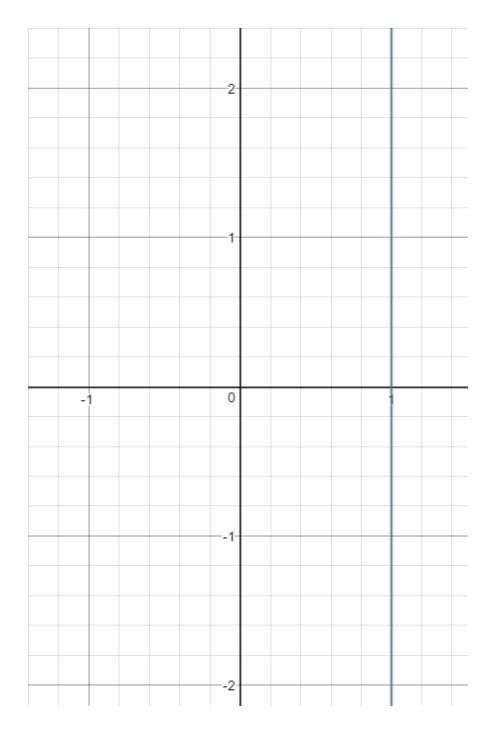
Näthän, että xxx:n on pakko olla 111 eikä se voi olla mikään muu. Heti kun valitset jonkun muun xxx:n arvon (kuten 222), niin tuo piste on pois suoralta. tarkastellaan kuitenkin yyy:tä. Huomaa, että yyy voi olla mikä tahansa, koska millä tahansa yyy-arvolla saamme pisteen, joka on suoralla, kunhan x=1x = 1x=1

Se tarkoittaa siis:

Domain: {x=1}Väli: {y∈\in∈R}

Jos sinulla oli paljon ongelmia piirtää kuvaajia saadaksesi toimialueen ja alueen, suosittelen käyttämään tätä laskinta.

https://www.desmos.com/calculator/2rnqgoa6a4

Se opettaa, miten lineaarinen yhtälö piirretään. Sinun tarvitsee vain kirjoittaa mmm:n ja bbb:n arvot. Sitten se piirtää suoran automaattisesti puolestasi! Tästä on hyötyä myös silloin, kun yrität löytää kaltevuuden leikkausmuodon.