Miten lasketaan esineen ripustavien köysien jännitys

Alhaalla olevasta kuvasta nähdään, että esineen nostamiseen tarvittava voima F on yhtä suuri kuin esineen paino W. Tämä ajatus on peruskäsite, joka on jännitysvoimakaavamme taustalla. Alla on myös esitetty esineen vapaakappalediagrammi, josta nähdään jousessa vaikuttavat jännitysvoimat T. Kuten näet, jännitysvoimat tulevat pareittain ja vastakkaisiin suuntiin:

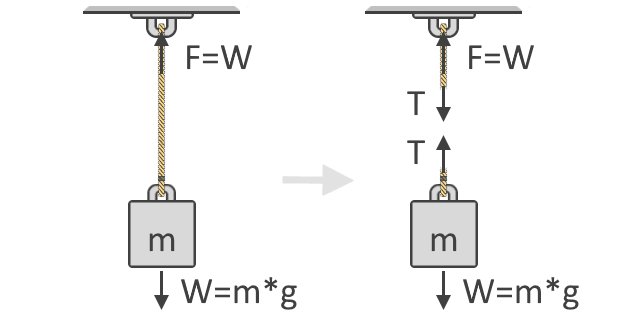
Newtonin toista liikelakia noudattaen voimme sitten ilmaista voimien yhteenlaskun käyttämällä esineen vapaakappalediagrammia, kuten yllä olevan kuvan oikealla puolella näkyy. Vapaakappalediagrammien avulla osoitamme kappaleeseen vaikuttavien voimien eri suunnat ja suuruudet. Tasapainossa kaikkien näiden voimien pitäisi olla nolla. Kun kaikki ylöspäin suuntautuvat voimat katsotaan positiivisiksi ja alaspäin suuntautuvat negatiivisiksi, yhtälömme on:

ΣF = 0 = T + (-W)
T = W
jossa paino, W, muuttuu negatiiviseksi, koska se suuntautuu alaspäin. Siirtämällä W yhtälön toiselle puolelle näemme nyt, että köyden jännitysvoima on yhtä suuri kuin sen kantaman esineen paino, kuten myös edellä on esitetty.

Jos käytämme useampia köysiä esineen nostamiseen, kokonaisjännitysvoima jakautuu köysien kesken. Kussakin köydessä oleva jännitysvoima riippuu niiden kulmista sen voiman suuntaan nähden, jota se vastustaa. Ymmärtääksemme tätä tarkemmin tarkastellaan toista vapaavartalokaaviota kahdella köydellä riippuvasta esineestä alla olevan kuvan mukaisesti:

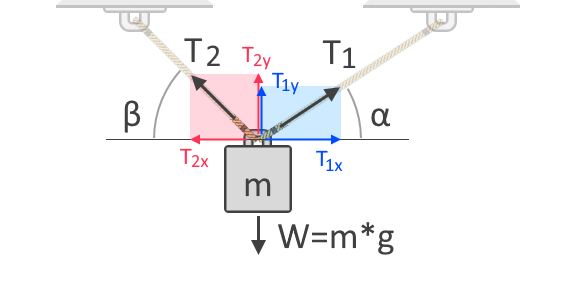
Yllä esitetyssä vapaavartalokaaviossa näemme jännitysvoimien vaaka- ja pystysuuntaiset komponentit, T₁, ja T₂. Voimat ovat vektoreita, eli niillä on aina sekä suuruus että suunta. Kuten kaikki vektorit, voimat voidaan ilmaista näillä komponenteilla, jotka antavat voiman vaikutuksen vaaka- ja pystyakselilla. T₁ₓ ja T₂ₓ ovat vastaavasti T₁:n ja T₂:n pystykomponentit. Toisaalta T₁ᵧ ja T₂ᵧ ovat vastaavasti samojen voimien pystykomponentteja. Koska painovoima vaikuttaa kappaleeseen pystyakselilla, meidän on otettava huomioon jännitysvoimien pystykomponentit voimien yhteenlaskussa seuraavasti:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Koska tiedämme myös jännitysvoimien kulmat, voimme trigonometristen funktioiden avulla ilmaista T₁ᵧ:n ja T₂ᵧ:n trigonometristen funktioiden avulla T₁:n ja T₂:n suhteen:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Voidaan myös sanoa, että jotta systeemi olisi tasapainossa, kappale ei saisi liikkua vaakasuorassa tai x-akselin suuntaisesti. Siksi T₁:n ja T₂:n vaakakomponenttien on tällöin oltava yhtä suuret kuin nolla. Myös trigonometrian avulla voimme ilmaista T₁ₓ ja T₂ₓ T₁:n ja T₂:n suhteen:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Jos jaamme molemmat puolet luvulla cos(α), saamme yhtälön, jossa T₁ ilmaistaan T₂:n ja kulmien suhteen:

T₁ = T₂ * cos(β) / cos(α)

Voidaan sitten käyttää tätä yhtälöä T₂:n ratkaisemiseen korvaamalla T₂ * cos(β) / cos(α) T₁:llä voimien summausyhtälössämme, kuten alla on esitetty:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Viimeiseksi, jos kerromme tämän koko yhtälön cos(β) / cos(α):llä, kuten johdimme T₁:n arvon T₂:n suhteen, ja sitten yksinkertaistamme kaiken, saamme tämän yhtälön:

T₁ = W / *
T₁ = W / *
T₁ = W /

Nyt tarvitsee vain tietää jännitysköysien kulmat vaakatason suhteen. Jos annetaan kulma pystysuoraan nähden, vähennä vain tämä kulma 90°:sta. Näin tekemällä saat kulman vaakatasoon nähden. Jos sinulle kuitenkin annetaan muita kulmien arvoja, jotka voivat olla suurempia kuin 90° tai jopa 180°, kannattaa tutustua referenssikulmalaskuriimme, joka auttaa sinua määrittämään tarvitsemasi kulman. Kun olemme määrittäneet muuttujien arvot jännitysvoimakaavoissamme, voimme nyt ratkaista jännitysvoimat.