Ising-malli on erityinen esimerkki termodynaamisesta systeemistä, ja se on mallijärjestelmä faasisiirtymien ymmärtämiseksi. Tiedättekö, kuinka monet biologit käyttävät niin paljon aikaa mitättömiin hedelmäkärpäsiin? No, fyysikot viettävät paljon aikaa Isingin mallin kanssa. Kuten professori Raghu avuliaasti kertoo meille, se on faasisiirtymien Drosophila.

Henkilökohtaisesti en ole hänen analogiansa suurin fani, koska minusta hedelmäkärpäset ovat ällöttäviä. Toivottavasti Isingin malli ei ole liian ällöttävä.

Motivaatio

Miksi meidän pitäisi käyttää niin paljon aikaa Isingin mallista puhumiseen?

• Se on yllättävän hyödyllinen auttaessaan meitä miettimään kaikenlaisia faasisiirtymiin liittyviä käyttäytymismalleja. Esimerkiksi:

  • Ising-mallissa esiintyy symmetrian murtumista matalalämpötilavaiheessa (josta juuri puhuimme)

  • sillä on erityinen ”kriittinen piste” tarkoin määritellyssä lämpötilassa (johon viittasimme veden faasidiagrammissa)

  • muitakin rikkaita ominaisuuksia.

• Se on yksi harvoista täsmällisesti ratkaistavista malleista, joissa voimme oikeasti laskea termodynaamisia suureita ja tulkita niitä.

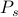  • Yleisesti termodynaamisten suureiden laskeminen on vaikeaa, koska joudumme laskemaan yhteen monta termiä. Muistathan ensimmäiseltä termotunniltamme, että voit ajatella tasapainosysteemiä monien tilojen muodostamana kokonaisuutena , joista jokainen on painotettu omalla todennäköisyydellään . Tässä kehyksessä havaitsemasi termodynaamiset suureet vastaavat kokonaisuuden keskiarvoja. Erityisesti, jos halutaan löytää jonkin havaintomäärän 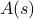ensemble-keskiarvo, on löydettävä summa 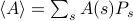, jossa summa kulkee kaikkien mahdollisten tilojen yli. Ongelma tässä, kuten muistat, on se, että termodynaamisen systeemin tilojen lukumäärä skaalautuu eksponentiaalisesti hiukkasten lukumäärän kanssa! Jopa kohtalaisen kokoisessa systeemissä on aivan liian monta tilaa, jotta tietokone voisi eksplisiittisesti laskea keskiarvon – puhumattakaan termodynaamisesta systeemistä, jossa 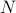on suuruusluokkaa .

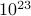  • Meidän on siis oltava ”nokkelia” laskeaksemme partitiofunktiota, ja meidän pitäisi olla kiitollisia eksaktisti ratkaistavissa olevista järjestelmistä!

• Isingin malli on yksinkertainen, mutta sitä voidaan soveltaa yllättävän moniin erilaisiin systeemeihin.

  • Tämä on ensimmäinen maistiaisemme universaalisuudesta – kriittisten ilmiöiden piirre, jossa sama teoria pätee kaikenlaisiin erilaisiin faasisiirtymiin, olipa kyse sitten nesteistä ja kaasuista tai magneeteista tai suprajohteista tai mistä tahansa. Fyysikot rakastavat tällaista yleistä käyttäytymistä, koska se viittaa jonkinlaiseen syvempään järjestykseen kaoottisessa maailmassamme.

Isingin mallin määritelmä

Isingin malli on matemaattinen malli, joka ei vastaa todellista fysikaalista järjestelmää. Se on valtava (neliönmuotoinen) paikkojen ristikko, jossa jokainen paikka voi olla yhdessä kahdesta tilasta. Merkitsemme jokaisen paikan indeksillä , ja kutsumme kahta tilaa ja . Sanoaksemme, että :nnen paikan tila on tilassa , kirjoitamme .

Nyt tämä määritelmä on valitettavan abstrakti ja epäfysikaalinen, joten meille fysiikkatieteilijöille on erittäin hyödyllistä, että meillä on mielessämme varsinainen systeemi, jotta voimme viitata johonkin eksplisiittiseen systeemiin ja rakentaa fysikaalisen intuition. Tässä on muutamia fysikaalisia systeemejä, joita Isingin malli voisi edustaa:

• Magneetti. Jokainen paikka edustaa tiettyä ’spiniä’ materiaalissa (parittamaton elektroni??), ja se on jos spin osoittaa alaspäin tai jos spin osoittaa ylöspäin. Jokainen spin toimii kuin minimagneetti, jolla on oma minimagneettinen momenttinsa; jos kaikki spinit ovat samassa linjassa, koko spinien ristikko käyttäytyy kuin iso magneetti, jolla on makroskooppinen nettomagneettinen momentti.

• Seos; vaikkapa messinki. Jokainen paikka on atomi hilassa; edustaa kupariatomia kyseisessä paikassa; edustaa sinkkiä.

• ”hilakaasu”. Jokainen paikka on hiukkasen mahdollinen sijaintipaikka; tarkoittaa, että paikka on tyhjä ja tarkoittaa, että paikka on hiukkasen miehittämä.

• Bakteerien pyörrevyöryritilät???

Käsitellään Isingin mallia toistaiseksi magneetin mallina. Se on varmasti karkeasti yksinkertaistettu ja lelumalli magneetista, mutta magneettianalogia voi kuitenkin auttaa ohjaamaan arvostettua fysikaalista intuitiotamme.

Hamiltonianin kokoaminen

Luonnollinen kysymys, joka voidaan esittää tästä magneetin Mikki Hiiri -mallista, on, mitä energiaa sillä on. Tarkemmin sanottuna haluamme kirjoittaa funktion, joka edustaa magneetissa olevien spinien jokaisen mahdollisen konfiguraation (eli mikrotilan) energiaa. Kuten tiedämme, tätä energiafunktiota kutsutaan Hamiltonianiksi.

Ising-mallissa Hamiltonianiin sisältyy kahdenlaisia vuorovaikutuksia:

• ulkoisen kentän termi. Kuten muistamme kvanttimekaniikasta, ulkoinen magneettikenttä voi jakaa spin-down- ja spin-up-tilan energiat niin, että toinen on energialtaan korkeampi ja toinen matalampi.

  • Kentän suuruus kuvaa sitä, kuinka voimakas kenttä on, eli se kertoo, kuinka paljon korkeampi energia toisella spinillä on kuin toisella.

  • Kentän merkki kertoo, onko spin-up vai spin-down edullisempi.

  • Koska jokainen yksittäinen spin tuntee ulkoisen kentän, meidän on laskettava summa kaikkien paikkojen yli, jotta löydämme kokonaispanoksen energiaan.

• Vuorovaikutustermi viereisten spinien välillä – ehkä ne haluavat kohdistua toisiinsa ja osoittaa samaan suuntaan, ehkä ne haluavat vastakkain kohdistua toisiinsa ja osoittaa eri tavoin. Fyysisesti voimme kuvitella, että tämä vuorovaikutus syntyy, koska magneetin jokainen spin on oma mini magneettidipolinsa, joka asettaa oman magneettikenttänsä, ja sen naapurit voivat tuntea tuon magneettikentän.

  • Koko kertoo, kuinka voimakkaasti viereiset spinit ovat kytköksissä toisiinsa – kuinka paljon ne haluavat (anti)kohdistua. Fysikaalisesti spin-spin-kytkennän voimakkuus voisi riippua esimerkiksi niiden välisestä etäisyydestä magetin hilassa.

  • Summan merkki kertoo, haluavatko naapurit mieluummin kohdistaa vai anti-kohdistaa. (Tekninen termi tälle on vastaavasti ferromagneettinen tai antiferromagneettinen). Fysikaalisesti se, onko materiaali jompaa kumpaa (vai ei kumpaakaan), riippuu spinien vuorovaikutuksen tarkoista kvanttimekaanisista yksityiskohdista.

  • Koska spin-spin-vuorovaikutus syntyy kahden spinin välille, joudumme laskemaan summan paikkaparien yli löytääksemme sen kokonaisvuorovaikutuksen energiaan.

Lisää vuorovaikutustermistä

Luonnollinen kysymys spin-spin-vuorovaikutustermistä on, mitkä spinit ovat kytköksissä mihinkin spiniin?

Jos käännymme taas takaisin magneetin fysikaaliseen kuvaan ja zoomaamme johonkin tiettyyn spiniin, odottaisimme spin-spin-vuorovaikutuksen voimakkuuden olevan voimakkaampi lähellä oleville spineille ja heikompi kaukana oleville spineille. Spin-spin-vuorovaikutuksen tarkka etäisyysriippuvuus on todennäköisesti varsin monimutkainen todellisissa magneeteissa.

Ising-mallissa teemme yksinkertaisimman mahdollisen oletuksen tämän spin-spin-vuorovaikutuksen luonteesta:

Muutamia kommentteja:

• Neliönmuotoisessa ulottuvuuden ristikossa jokaisella paikalla on 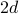lähimpiä naapureita: vasemmalla ja oikealla yhdessä ulottuvuudessa, ylhäällä ja alhaalla, kun lisätään toinen ulottuvuus, jne…

• Edellytämme, että vuorovaikutus on isotrooppista – kaikkia naapureita kohdellaan tasavertaisesti suunnasta riippumatta.

• Puhumme usein lähimmän naapurin vuorovaikutuksesta kahta ristikon paikkaa yhdistävän sidoksen energiana.

• Kun summaamme vierekkäisten paikkaparien yli, symbolisesti kirjoitamme pienet kulmasulkeet indeksien ympärille kuvaamaan ”lähintä naapuria”.

Lähimmän naapurin vuorovaikutusten mukava seuraus on se, että kun etsimme jonkin spiinikonfiguraation kokonaisenergiaa, sen sijaan, että summaisimme kaikkien mahdollisten paikkaparien yli, summaamme vain toistensa vierekkäisten paikkaparien yli.

Nyt kun olemme keskustelleet kaikista näistä asioista, olemme valmiita kirjoittamaan varsinaisen lausekkeen Hamiltonianille. (Halusin selittää ja tulkita fysiikkaa ennen Hamiltonianin kirjoittamista, jotta symboleissa olisi jonkinlaista järkeä.)

Ising-mallin hamiltonilainen

Ising-mallin hamiltonilainen voidaan kirjoittaa seuraavasti

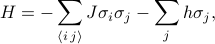
joissa edustaa spin-spin-vuorovaikutusta, ulkoista kenttää ja 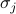yksittäisiä spinejä kullakin ristikon paikalla. Ensimmäinen summa on kaikkien viereisten ristikkopaikkaparien (eli sidosten) summa; se edustaa spinien välisiä vuorovaikutuksia. Toinen summa on kaikkien itse ristikkokohtien summa; se edustaa ulkoista kenttää, joka yrittää kohdistaa kaikki spinit yhteen suuntaan.

Jatketaan Ising-mallin termodynamiikkaan.