by Marco Taboga, PhD
Tapahtuman indikaattorifunktio on satunnaismuuttuja, joka saa arvon 1, kun tapahtuma tapahtuu, ja arvon 0, kun tapahtumaa ei tapahdu. Indikaattorifunktioita käytetään usein todennäköisyysteoriassa notaation yksinkertaistamiseksi ja teoreemojen todistamiseksi.

Määritelmä
Seuraavassa on muodollinen määritelmä.
Määritelmä Olkoon  otosavaruus ja
otosavaruus ja  tapahtuma. Tapahtuman
tapahtuma. Tapahtuman  indikaattorifunktio (tai indikaattorin satunnaismuuttuja), jota merkitään
indikaattorifunktio (tai indikaattorin satunnaismuuttuja), jota merkitään  , on satunnaismuuttuja, joka määritellään seuraavasti:
, on satunnaismuuttuja, joka määritellään seuraavasti: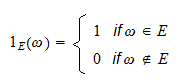
Vaikka tapahtuman  indikaattoria merkitään yleensä
indikaattoria merkitään yleensä  :llä, joskus sitä merkitään myös
:llä, joskus sitä merkitään myös  :llä, jossa
:llä, jossa  on kreikkalainen kirjain Chi.
on kreikkalainen kirjain Chi.
Esimerkki Heitetään noppaa ja yksi kuudesta numerosta 1-6 voi ilmestyä kuvapuoli ylöspäin. Näyteavaruus on  Määritellään tapahtuma
Määritellään tapahtuma  , jota kuvaa lause ”Parillinen luku ilmestyy kuvapuoli ylöspäin”. Satunnaismuuttuja, joka saa arvon 1, kun parillinen luku ilmestyy kuvapuoli ylöspäin, ja muuten arvon 0, on tapahtuman
, jota kuvaa lause ”Parillinen luku ilmestyy kuvapuoli ylöspäin”. Satunnaismuuttuja, joka saa arvon 1, kun parillinen luku ilmestyy kuvapuoli ylöspäin, ja muuten arvon 0, on tapahtuman  indikaattori. Tämän indikaattorin tapauskohtainen määritelmä on
indikaattori. Tämän indikaattorin tapauskohtainen määritelmä on
Yllä olevasta määritelmästä voidaan helposti nähdä, että  on diskreetti satunnaismuuttuja, jolla on tuki
on diskreetti satunnaismuuttuja, jolla on tuki  ja todennäköisyysmassafunktio
ja todennäköisyysmassafunktio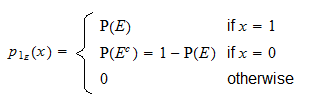
ominaisuudet
Indikaattorifunktiot nauttivat seuraavia ominaisuuksia.
Tehot
 :n
:n  :nnen potenssin
:nnen potenssin  arvo on
arvo on  :
: koska
koska  voi olla joko
voi olla joko  tai
tai  ja
ja
Odotusarvo
Odotusarvo  on
on  :
: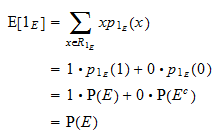
Varianssi
Varianssi  on
on  . Tavanomaisen varianssin kaavan ja yllä olevan potenssiominaisuuden ansiosta saadaan
. Tavanomaisen varianssin kaavan ja yllä olevan potenssiominaisuuden ansiosta saadaan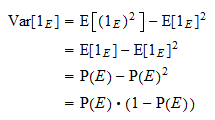
Ristiriidat
Jos  ja
ja  ovat kaksi tapahtumaa, niin
ovat kaksi tapahtumaa, niin koska:
koska:
-
jos
 , niin
, niin  ja
ja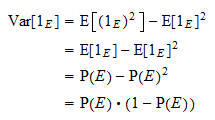
-
jos
 , niin
, niin ja
ja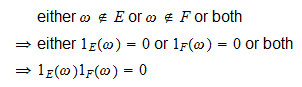
Nollatodennäköisyystapahtumien indikaattorit
Olkoon  nollatodennäköisyystapahtuma ja
nollatodennäköisyystapahtuma ja  integroitava satunnaismuuttuja. Silloin,
integroitava satunnaismuuttuja. Silloin, Vaikka tämän tosiasian tiukka todistaminen ei kuulu tähän johdantoesitykseen, tämän ominaisuuden pitäisi olla intuitiivinen. Satunnaismuuttuja
Vaikka tämän tosiasian tiukka todistaminen ei kuulu tähän johdantoesitykseen, tämän ominaisuuden pitäisi olla intuitiivinen. Satunnaismuuttuja  on nolla kaikissa otospisteissä
on nolla kaikissa otospisteissä  paitsi mahdollisesti pisteissä
paitsi mahdollisesti pisteissä  . Odotusarvo on painotettu keskiarvo niistä arvoista, joita
. Odotusarvo on painotettu keskiarvo niistä arvoista, joita  voi saada, missä jokainen arvo on painotettu sille kuuluvalla todennäköisyydellä. Nollasta poikkeavat arvot, joita
voi saada, missä jokainen arvo on painotettu sille kuuluvalla todennäköisyydellä. Nollasta poikkeavat arvot, joita  voi ottaa, painotetaan nollatodennäköisyyksillä, joten
voi ottaa, painotetaan nollatodennäköisyyksillä, joten  :n täytyy olla nolla.
:n täytyy olla nolla.
Ratkaistuja harjoituksia
Alla on muutamia harjoituksia selitettyine ratkaisuineen.
Harjoitus 1
Tarkastellaan satunnaismuuttujaa  ja toista satunnaismuuttujaa
ja toista satunnaismuuttujaa  , joka on määritelty
, joka on määritelty  funktiona.
funktiona.
Ilmaise  käyttämällä tapahtumien
käyttämällä tapahtumien  ja
ja  indikaattorifunktioita.
indikaattorifunktioita.
Kirjoita  :lla tapahtuman
:lla tapahtuman  indikaattori ja kirjoita
indikaattori ja kirjoita  :llä tapahtuman
:llä tapahtuman  indikaattori. Voimme kirjoittaa
indikaattori. Voimme kirjoittaa  seuraavasti:
seuraavasti: 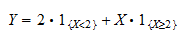
Harjoitus 2
Olkoon  positiivinen satunnaismuuttuja eli satunnaismuuttuja, joka voi saada vain positiivisia arvoja. Olkoon
positiivinen satunnaismuuttuja eli satunnaismuuttuja, joka voi saada vain positiivisia arvoja. Olkoon  vakio. Osoita, että
vakio. Osoita, että  missä
missä  on tapahtuman
on tapahtuman  indikaattori.
indikaattori.
Huomaa ensin, että tunnuslukujen  ja
ja  summa on aina yhtä suuri kuin
summa on aina yhtä suuri kuin  :
: Sen seurauksena voimme kirjoittaa
Sen seurauksena voimme kirjoittaa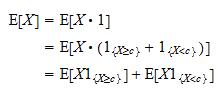 Huomaa nyt, että
Huomaa nyt, että  on positiivinen satunnaismuuttuja ja että positiivisen satunnaismuuttujan odotusarvo on positiivinen:
on positiivinen satunnaismuuttuja ja että positiivisen satunnaismuuttujan odotusarvo on positiivinen: Siten,
Siten,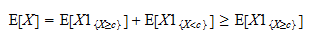
Harjoitus 3
Olkoon  tapahtuma ja merkitään sen indikaattorifunktiota
tapahtuma ja merkitään sen indikaattorifunktiota  . Olkoon
. Olkoon 
 :n komplementti ja merkitään sen indikaattorifunktiota
:n komplementti ja merkitään sen indikaattorifunktiota  . Voitko ilmaista
. Voitko ilmaista  funktiona
funktiona  ?
?
Kahden tunnusluvun summa on aina yhtä suuri kuin  :
: Therefore,
Therefore,
How to cite
Please cite as:
Taboga, Marco (2017). ”Indikaattorifunktiot”, Luentoja todennäköisyysteoriasta ja matemaattisesta tilastotieteestä, kolmas painos. Kindle Direct Publishing. Verkkoliite. https://www.statlect.com/fundamentals-of-probability/indicator-functions.