Miten teemme Guinier-sovituksen?¶
Guinier-approksimaatio pätee vain, kun eksponentti \(\exp(-q^2 R_g^2 /3)\)\)\)\)on pieni. Tämä tarkoittaa, että hyvän Guinier-sovituksen aikaansaamiseksi meidän täytyyqRg:n olla riittävän pieni. qRg-arvo, jossa Guinierin approksimaatio alkaa epäonnistua tietylle sirontaprofiilille, riippuu sironnan yleisestä muodosta. Alla on kuva, jossa esitetään Guinierin approksimaatio (musta) ja sirontaintensiteetti pallolle, ohuelle sauvalle ja ohuelle kiekolle (joilla kaikilla on sama Rg).
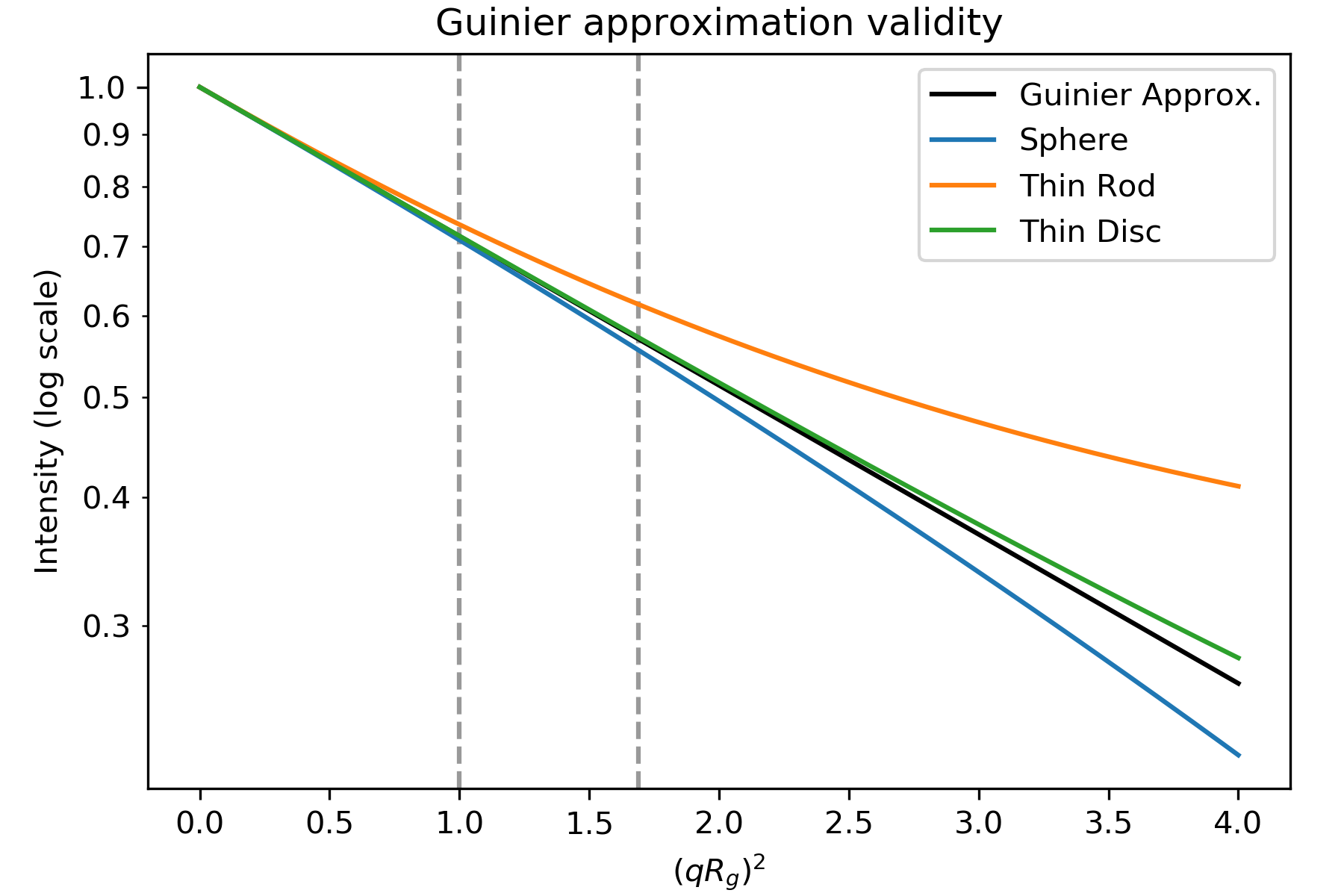
Kuvio perustuu kuvaan 3.3 teoksessa . Intensiteetti taulukon 3.4 taulukon 3.4 geometrisille muodoille. Katkoviivat ovat qRg:n ollessa 1.0 ja 1.3((qRg) 2:n ollessa 1.0 ja 1.69).
Kuten näette, sauvan sirontaintensiteetti vastaaGuinierin approksimaatiota vain \(qR_g\sim 1.0\) asti, pallon \(qR_g\sim 1.3\) asti ja kiekon \(qR_g\sim 1.7\) asti. Näin ollen hiukkasten yleisestä muodosta riippuen on sovitettava eri määrät matalan q:n dataa, jotta saadaan hyvä Guinier-sovitus. (Huomaa: kuvaajan x-akseli on (qRg) 2, joten \(qR_g\sim 1.3\) näkyy katkoviivana 1.69:n kohdalla)
Käytännössä sovitamme sekä pallomaisia (pallomaisia että kiekkomaisia) objekteja \(qR_g\sim 1.3\) asti, kun taas pitkälle ulottuvia (sauvamaisia) objekteja sovitamme \(qR_g\sim 1.0\) asti. Nämä arvot valittiin siten, että niissä on <10 prosentin virhe, joka johtuu todellisen muodon poikkeamasta Guinierin approksimaatiosta.Syy siihen, että hyväksymme näin suuren poikkeaman, on se, että epävarmuutta syntyy myös siitä, että sovitetaan vähemmän datan pisteitä, joten on tehtävä kompromissi sen välillä, kuinka hyvin approksimaatio toimii (sovitus pienempään maksimi-qRg:hen) ja kuinka hyvin pystytään sovittamaan dataa (sovitus suurempaan maksimi-qRg:hen).
Guinier-sovituksen alue on siis ihanteellisesti varhaisimmasta käytettävissä olevasta q-arvosta maksimi qRg:n arvoon 1,0 tai 1,3 asti. Ottaen kuitenkin huomioon, että Rg on johdettu Guinierin sovituksesta, miten määritetään oikea suurin q-arvo sovituksen loppupäähän? Vastaus on, että Guinier-sovitus tehdään iteratiivisesti:
- Arvioi sovituksen aloitusmaksimi q-arvo.
- Lasketaan Guinier-sovitus ja saadaan Rg.
- Jos qmaxRg > 1.3 (tai 1.0), pienennä maksimi q:ta. JosqmaxRg < 1.3 (tai 1.0), suurenna maksimi q:ta.
- Toista vaiheet 2 ja 3, kunnes konvergoit lopulliseen maksimi q:hen.
Useimmat ohjelmistot tekevät nykyään tämän iteratiivisen haun puolestasi, ja hyvälaatuisille aineistoille ne antavat sinulle kohtuullisen q:n maksimiarvon, joka saattaa tarvita vain hieman manuaalista hienosäätöä.
Guinier-sovituksen q:n minimiarvo määräytyy tavallisesti aineistossasi olevan q:n pienimmän saatavissa olevan arvon mukaan, joka määräytyy mittalaitteessa, jolla teet mittauksen.On kuitenkin tärkeää, että q:n minimiarvo on tarpeeksi pieni, jotta Guinier-sovitukselle saadaan kohtuullisesti vaihteluväliä. Tyypillisesti qRg:n vähimmäisarvon pitäisi olla\(qR_g\leq 0.65\), mutta pallomaisissa järjestelmissä voi olla hyvä olla\(qR_g\leq 1.0\). Tämä tarkoittaa, että tarvittava q:n vähimmäisarvo riippuu mitatun järjestelmän koosta. Joissakin tapauksissa, kun kyseessä ovat erityisen suuret järjestelmät, saatat joutua tietoisesti etsimään mittalaitetta, joka pystyy mittaamaan riittävän pienelle q:lle.
Jos aineistossasi on laatuongelmia pienellä q:lla, jotka voivat johtua edellä luetelluista ongelmista, saatat huomata, että näiden tietojen jättäminen pois sovituksesta voi parantaa sovituksen laatua. Vaikka tämä voi olla hyväksyttävää, sinun on toimittava varovaisesti näin tehdessäsi ja näytettävä aina koko datan vaihteluväli kuvaajissa.Hyväksyttävin tapaus, jossa näin voi tapahtua, on, kun muutamat ensimmäiset pisteet ovat joko liian korkeita tai liian matalia, mutta loppuosa vaihteluvälistä sopii täydellisesti (katso jäljempänä hyvän sovituksen kriteerit). Tällöin niillä parilla pisteellä, jotka ovat lähimpänä säteen pysäytyspistettä, voi olla huonot tilastot tai suurempi instrumentaalinen taustasironta, ja ne voidaan yleensä jättää turvallisesti huomiotta.