Jatkuvassa näyteavaruudessa tapahtuvat satunnaistapahtumat voivat vedota geometrisiin mielikuviin ainakin kahdesta syystä: ongelman luonteen tai ratkaisun luonteen vuoksi.

Jotkut ongelmat, kuten Buffonin neula, Linnut langalla, Bertrandin paradoksi tai kolmeksi palaseksi murtuneen kepin ongelma, syntyvät luonteensa vuoksi geometrisessa ympäristössä. Jälkimmäinen sallii myös useita uudelleenmuotoiluja, jotka edellyttävät geometristen kuvioiden pinta-alojen vertailua. Yleisesti voidaan ajatella, että geometriset todennäköisyydet ovat ei-negatiivisia suureita (enintään 1), jotka osoitetaan tietyn alueen osa-alueille tiettyjen sääntöjen mukaisesti. Jos funktio μ on tämän osoittamisen ilmaus, joka on määritelty tietylle alueelle D, vaadimme esimerkiksi

0 ≤ μ(A) ≤ 1, A ⊂ D ja
μ(D) = 1

Funktiota μ ei yleensä määritellä kaikille A ⊂ D:lle. Ne D:n osajoukot, joille μ on määritelty, ovat satunnaistapahtumia, jotka muodostavat tietyt näyteavaruudet. Hyvin usein μ määritellään pinta-alojen suhteen avulla siten, että jos σ(A) määritellään joukon A ”pinta-alaksi”, voidaan asettaa μ(A) = σ(A) / σ(D).

Ongelma 1

Kaksi ystävää, jotka kulkevat metrolla työpaikalleen samalta asemalta, saapuvat asemalle tasaisen sattumanvaraisesti aamulla kello 7 ja 7.20 välillä. He ovat valmiita odottamaan toisiaan 5 minuuttia, jonka jälkeen he nousevat junaan joko yhdessä tai yksin. Mikä on todennäköisyys, että he tapaavat asemalla?

Kartesiolaisessa koordinaatistossa (s, t) neliö, jonka sivu on 20 (minuuttia), edustaa kaikkia mahdollisuuksia kahden ystävän aamuiseen saapumiseen metroasemalle.

Harmaata aluetta A rajoittaa kaksi suoraa, t = s + 5 ja t = s – 5, joten A:n sisällä |s – t| ≤ 5. Tästä seuraa, että kaksi ystävää tapaa toisensa vain, jos heidän saapumisensa s ja t osuvat alueelle A. Todennäköisyys sille, että näin tapahtuu, saadaan A:n pinta-alan ja neliön pinta-alan suhteella:

/ 400 = 175/400 = 7/16.

Ongelma 2

(.)

Kolme pistettä A, B, C sijoitetaan sattumanvaraisesti ympyrälle, jonka säde on 1. Millä todennäköisyydellä ΔABC on terävä?”

Kiinnitetään piste C. Pisteiden A ja B sijainnit määritellään tällöin C:stä kahteen suuntaan ulottuvien kaarien α ja β avulla. A priori tiedämme, että 0 < α + β < 2π. Ongelmamme kannalta suotuisat α:n ja β:n arvot (koska ne vastaavat teräviä kulmia) ovat 0 < α < π ja 0 < β < π. Niiden summa ei voi olla pienempi kuin π, koska silloin kulma C olisi tylppä, joten α + β > π. Tilanne on esitetty seuraavassa kuvassa, jossa neliön sivu on 2π.

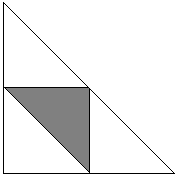
Regio D on kolmen puolitason leikkauspiste: 0 < α, 0 < β ja α + β < 2π. Tämä on yllä olevan kaavion iso kolmio. Suotuisat tapahtumat kuuluvat tummennettuun kolmioon, joka on puolitasojen α < π, β < π ja α + β > π leikkauspiste. Niiden pinta-alojen suhde on ilmeisesti 1/4.

Huomaa nyt, että ellei satunnainen kolmio ole terävä, sitä voidaan ajatella tylpäksi, koska todennäköisyys sille, että kaksi kolmesta pisteestä A, B, C muodostaa halkaisijan, on 0. (Jotta BC olisi halkaisija, pitäisi olla α + β = π, joka on suora, jolloin nolla on ainoa mahdollinen pinta-alan määritys). Näin ollen voidaan sanoa, että todennäköisyys sille, että ΔABC on tylppä, on 3/4. Jos kyseessä on tylppä kolmio, ympyrä voidaan jakaa kahteen puolikkaaseen, jolloin kolmio sijaitsee kokonaan toisella puolikkaalla. Tästä seuraa, että 3/4 on vastaus seuraavaan kysymykseen:

Kolme pistettä A, B, C sijoitetaan satunnaisesti ympyrälle, jonka säde on 1. Mikä on todennäköisyys, että kaikki kolme sijaitsevat puoliympyrällä?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, ongelma 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions (Todennäköisyysteorian ongelmia, matemaattinen tilastotiede ja satunnaisfunktioiden teoria), Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometrinen todennäköisyys

• Geometriset todennäköisyydet
• Ovatko useimmat kolmiot tylsiä?
  • Kahdeksan valintaa kuudessa sektorissa
  • Kolme satunnaista pistettä ympyrällä
• Geometriset todennäköisyydet
  • Kepin murtaminen kolmeen osaan (trilineaariset koordinaatit)
  • Kepin murtaminen kolmeen osaan. Ratkaisu kartesiankoordinaatistossa
• Bertrandin paradoksi
• Linnut langalla (ongelma ja interaktiivinen simulaatio)
  • Linnut langalla: Nathan Bowlerin ratkaisu
  • Birds on a Wire. Ratkaisu: Mark Huber
  • Birds on a Wire: probabilistinen simulaatio. Ratkaisu: Moshe Eliner
  • Birds on a Wire. Ratkaisu: Stuart Anderson
  • Birds on a Wire. Ratkaisu: Bogdan Lataianu
• Buffonin nuudelisimulaatio
• Sadepisaroiden keskiarvoistaminen – harjoitus geometrisesta todennäköisyydestä
  • Sadepisaroiden keskiarvoistaminen, osa 2
• Suorakulmio shakkilaudalla: Johdanto
• Tikkujen merkitseminen ja katkaiseminen
• Sattumanvaraiset pisteet segmentillä
• Puoliympyrän peittävyys
• Puoliympyrän peittävyys
• Yllekkäiset satunnaisvälit
• Sattumanvaraiset välit
• Satunnaisvälit joissa on yksi hallitseva
• Pisteet neliöruudukossa
• Litteät todennäköisyydet pallolla
• Todennäköisyys kolmiossa

|Yhteydenpito|||Etusivu|||Sisältö|||Ylöspäin|

Copyright © 1996-2018 Alexander Bogomolny