Sähkövarauksesta ja sähkökentästä tiedämme lähes kaiken, mutta entä Gaussin laki ? Gaussin laki on tärkeä aihe tässä luvussa, mutta ennen kuin menemme Gaussin lakiin, meidän on ymmärrettävä, mikä on Gaussin pinta ja miten Gaussin pinta määritetään?
Ennen kuin jatkamme siitä, miten Gaussin pinta määritetään, ymmärtäkäämme ensin, mikä on Gaussin pinta.

Mikä on Gaussin pinta?

Pinta, jossa sähkökentän (E) ja pinta-alavektorin (A) välinen kulma (ө) on aina vakio jokaisessa pisteessä tällainen pinta tunnetaan Gaussin pintana.
Et ehkä ymmärtänyt termiä sähkökenttä tai pinta-alavektori. Joten tietääksesi sähkökentästä minulla on oma artikkeli sähkövarauksesta ja sähkökentästä, joten lue myös.
Me tiedämme, että vektorisuureella on suuruus ja suunta, joten pinta-alavektorit ovat tasopinnan vektoreita, joiden suuruus on pinnan pinta-ala ja suunta on kohtisuorassa pintaa vastaan.

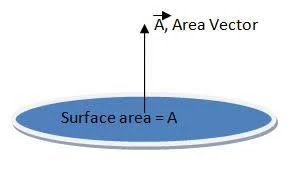
Pinta-alavektori

Miten tunnistat Gaussin pinnan, jos näet sellaisen?

Miten määritetään Gaussin pinta?

Tiedämme, että Gaussin pinta noudattaa Gaussin lakia ja sähkökentän (E) ja pinta-alavektorin (A) välinen kulma (ө) on aina sama jokaisessa pisteessä. Määrittääksemme Gaussin pinnan meidän on siis vain tarkistettava, onko kulma (ө) pinnan jokaisessa pisteessä sama vai ei.
Gaussin laki:

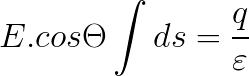
Tässä ovat vaiheet Gaussin pinnan määrittämiseksi:
Vaihe 1: Valitaan pinta kappaleesta tai esineestä
Niin usein ihmiset menevät sekaisin ja alkavat tarkistaa, onko kulma sama kaikissa pisteissä kappaleessa vai ei. Sinun on oltava selvillä siitä, että haluamme tunnistaa, onko kappaleen pinta Gaussin pinta vai ei, ja siksi tarkistamme kulman (ө) jokaisessa pisteessä pinnalla emmekä koko kappaleen jokaisessa pisteessä.

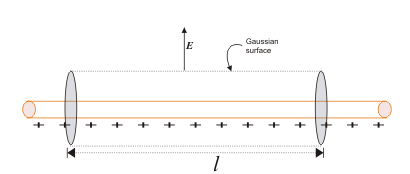
Pinnan tunnistaminen

Yllä olevassa kuvassa tarkastelemme varjostamatonta aluetta saadaksemme selville, onko se Gaussin pinta vai ei, ja varjostettua aluetta ei oteta huomioon, koska meidän on selvitettävä, onko kappaleen pinta Gaussin pinta vai ei.
P.s.: Se tarkoittaa, että kappaleella voi olla enemmän kuin 1 Gaussin pinta.
Vaihe 2: Tarkista sähkökentän suunta (E)
Nyt kun pinta on päätetty, on tarkistettava sähkökentän suunta pinnasta.
Miten sähkökentän viivat lähtevät pinnasta.

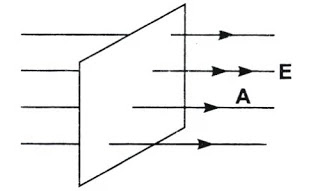
Sähkökentän suunta

Jos et tiedä sähkökentästä tai sähkökenttäviivoista, meillä on toinenkin artikkeli tästä, lue myös se, koska olemme toimittaneet käsinkirjoitettuja muistiinpanoja jokaisen sähkökentän ja Gaussin pinnan ja lain derivaation kanssa. Klikkaa tästä lukeaksesi tuon artikkelin
Vaihe 3: Tarkista pinta-alavektori (A)
Sähkökentän suunnan tarkistamisen jälkeen sinun on tarkistettava pinnan pinta-alavektori. Pinta-alavektori on itse asiassa vektori, jonka suunta on aina kohtisuorassa pintaa vastaan.
Vaihe 4: Tarkista pinta-alavektorin (A) ja sähkökentän (E)
Sähkökentän ja pinta-alavektorin suunnan määrittämisen jälkeen on siis aika selvittää niiden välinen kulma (ө).

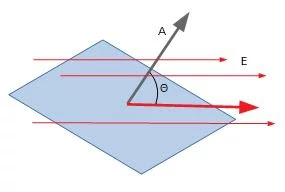
Pinta-alavektorin ja sähkökentän välinen kulma

Tarkistetaan, onko molempien välinen kulma sama kaikissa pisteissä. Jos Kyllä! niin se on Gaussin pinta.

Noh, yksi kysymys, joka on ehkä iskenyt sinuun, on, miksi on tarpeen määrittää Gaussin pinta, miksi se on niin tärkeä?

Miksi on tarpeen määrittää Gaussin pinta ja miten se auttaa meitä?

Gaussin pinta auttaa meitä arvioimaan sähkökenttää, joka johtuu erilaisesta varausjakaumasta.
Jos haluat löytää tietoa sähkökentän arvioimisesta, joka johtuu erilaisesta varausjakaumasta, minulla on henkilökohtaisia muistiinpanojani, jotka on ladattu tälle sivustolle. Klikkaa tästä siirtyäksesi artikkeliin ladataksesi muistiinpanot.

Joitakin esimerkkejä Gaussin pinnasta:

Eli joitakin esimerkkejä Gaussin pinnasta ovat:
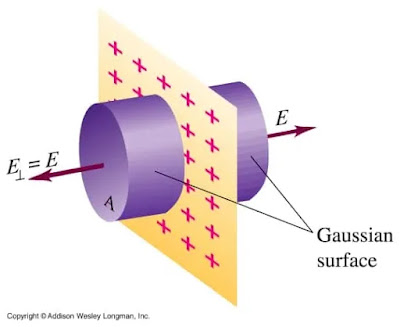
1. Kuvitteellinen sylinterimäinen Gaussin pinta, joka on luotu suoran varatun johtimen aiheuttaman sähkökentän selvittämiseksi. Löydät tämän johdannon myös muistiinpanoistamme 🙂

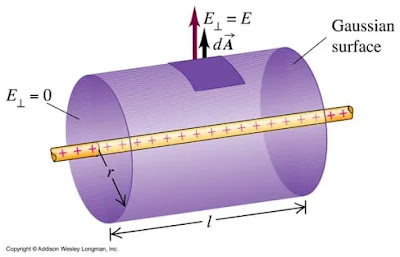
2. Kuvitteellinen sylinterimäinen Gaussin pinta, joka on luotu tasaisen varatun levyn aiheuttaman sähkökentän selvittämiseksi. Löydät tämänkin derivaation muistiinpanoistamme 🙂