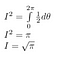Lordi Kelvin kirjoitti integraalista: ”
Hyvää 😉
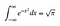
Okei, oletan, että osaat integraation ja differentioinnin perusteet. Seuraavassa lisätään hieman intuitiota nokkeliin temppuihin, jotka tulevat myöhemmin. Älä huoli, jos osa tästä on hieman hämmentävää, yritä vain saada tuntumaa siihen, mitä tapahtuu.
Strategiana tässä on tehdä nokkela substituutio. Mutta teemme substituution kahdella muuttujalla. Voit visualisoida tämänhetkisen ongelman käyrän alapuolisen pinta-alan laskemiseksi
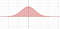
Mutta näytämme, että ongelman voi muuttaa tilavuuden laskemiseksi.
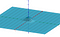
Tilavuuden laskemiseksi käytämme hieman erilaista muuttujanvaihtokaavaa kuin tavallisissa integraaleissa. Käytämme polaarikoordinaatteja. Tämä ilmaisee x- ja y-koordinaatit säteen ja kulman muodossa. Geogebrassa on mukava interaktiivinen tapa nähdä se täällä

Sitten käytämme polaarikoordinaattien maagista perusluvunmuutoskaavaa.
Käyrän alapuolisen pinta-alan laskemisessa meillä oli elementti ’dx’, joka edustaa pientä etäisyyttä x-akselilla. Tilavuutta laskettaessa meillä on dx dy, joka on kuin pieni suorakulmio, jonka sivujen pituudet ovat dx ja dy. Käytämme sitten näitä perusteita luodaksemme sarjan laatikoita, jotka arvioivat tilavuuden. Tämä on helpointa nähdä alla olevan visualisoinnin avulla. Integraali on näiden approksimaatioiden raja-arvo.
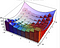
Kun sen sijaan käytämme polaarikoordinaatistoa, meillä on alla hieman erilainen alue-elementti. Alla dA on pinta-alaelementti. Kulman ja säteen pienillä muutoksilla tätä pinta-alaelementtiä voidaan approksimoida yhä paremmin suorakulmiolla, jonka sivujen pituudet ovat dr ja r*dtheta. Jos osaat jonkin verran geometriaa, pienillä theta-arvoilla sin(theta) approksimoituu hyvin thetalla, jolloin voit todistaa alla olevan tuloksen.
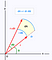
Integraalin ratkaiseminen
Ensin annamme integraalillemme nimen. Kutsumme sitä nimellä I.
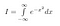
Huomaa, että x on pelkkä ’tyhjä muuttuja’. Alue on olemassa riippumatta siitä, mitä muuttujan nimeä käytämme. Voimme siis kirjoittaa myös seuraavat kaksi yhtälöä
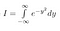
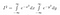
Nyt kun I on vain vakio, vaikkakaan sellainen, jonka arvoa emme vielä tiedä, voimme käyttää normaaleja sääntöjämme vakion tuomiseen integraalin sisälle
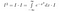
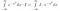
Vaikka tähän mennessä emme ole vielä tehneet kovinkaan paljoa oleellista. Nyt mietimme tarkkaan, mitä integraali tarkoittaa. Otamme funktioiden integraaleja. Jos kaksi funktiota ottaa kaikkialla saman arvon, ne ovat samoja ja niillä on sama pinta-ala. Tätä ajatellen voimme tehdä seuraavat manipulaatiot, jos katsomme I*exp(-x²):n funktioksi x:stä eli joksikin, joka ottaa syötteenä x:n arvot ja antaa tuloksena luvun.
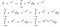
Okei, siinä oli paljon omaksuttavaa. Ensimmäisellä rivillä kirjoitimme vain I:n uudelleen integraalimuodossaan eri muuttujan nimellä. Toisella rivillä käsittelemällä I*exp(-x²) funktiona tajusimme, että voimme tuoda exp(-x²):n dy-integraalin sisälle, ja tämä antaisi edelleen saman lähtöarvon mille tahansa x:n tuloarvolle. Lopuksi käytimme eksponentiointisääntöjä.
Kirjoittamalla tämän kokonaisuudessaan, meillä on nyt
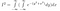
Seuraavaksi tulee tappava oivallus. Edellä pelleilimme muuttujien nimien ja funktion esittämisen kanssa. Nyt vaihdamme näkökulmaa: tämä lauseke edustaa myös integraalia exp(-(y²+x²)) koko 2D-tasolla, jonka pinta-alaelementti dA = dx dy. Eli dx dy on pieni suorakulmio tasossa, ja exp(-(y²+x²)) on korkeus tuon suorakulmion yläpuolella.
Seuraavaksi käytetään aiempia polaarikoordinaatiston oivalluksia
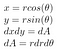
As sin² + cos² = 1, kun kaikki on kytketty, saadaan
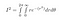
r vaihtelee 0:sta äärettömään ja theta vaihtelee 0:sta 2*pi:hen, koska tämä kattaa koko 2D-tason: minkä tahansa pisteen säde on pienempi kuin ääretön ja kulma välillä 0-2pi radiaania.
Voidaan arvioida sisäinen integraali ketjusäännön avulla
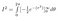
Ja, luvattuun maahan olemme nyt päässeet: