Mitä tiedät äärettömyydestä? Olet varmaan kuullut luvusta, joka on suurin mahdollinen tai mahdottoman suuri luku.
Voidakseni selittää äärettömyydet, minun on ensin määriteltävä joitakin termejä.
Luvut ovat lukumääriä, joita käytetään laskemiseen. Kokonaislukujen joukoksi määritellään kaikki luvut, joilla ei ole murto-osia. Joitakin esimerkkejä ovat:
Ääretön on käsite kohteesta, joka on luonnollisten lukujen ulottumattomissa. Sen käsitteellisti ensimmäisen kerran venäläinen matemaatikko nimeltä Georg Cantor, joka paitsi esitteli äärettömyyden, myös paljasti, että on olemassa useita äärettömyyksiä.
Cantor esitti kiistanalaisen todisteen äärettömyydestä, jonka mukaan jotkut äärettömyydet olivat suurempia kuin toiset. Aluksi tämä voi tuntua mahdottomalta – miten jokin objekti voi olla suurempi kuin toinen ääretön objekti?

Cantor perusti todisteensa näennäisesti hyödyttömältä tuntuvaan matematiikan haaraan: Joukkoteoriaan. Joukko on kokoelma objekteja – esimerkiksi meillä voi olla joukko, joka sisältää 1, 2 ja 3. Näitä joukon objekteja kutsutaan alkioiksi.
Matemaattisessa notaatiossa tämä näyttäisi seuraavalta:
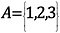
Elementtien lukumäärä tässä joukossa eli joukon kardinaalisuus on 3.
Tämä merkitään seuraavasti:
Yksi tapa, jolla voimme todeta tämän, on laskea toisen joukon alkioiden lukumäärä. Näemme selvästi, että tässäkin joukossa on kolme alkiota, joten tiedämme, että ne ovat samankokoisia.
Toinen tapa on verrata toista joukkoamme B ensimmäiseen joukkoomme A kartoittamalla.
Voidaan kartoittaa joukon A ensimmäinen alkio , 1, joukon B ensimmäiseen alkioon, tuoli.
Voidaan kartoittaa toinen alkio joukosta A, 2, joukon B toiseen alkioon, pöytä.
Voidaan kartoittaa kolmas alkio joukosta A, 3, joukon B kolmanteen alkioon, hattu.
Koska jokainen alkio joukosta A kartoitetaan täsmälleen yhteen alkioon joukosta B, joukot ovat samankokoisia.
Katsotaan nyt äärettömiä joukkoja. Alussa mainittu kokonaislukujen joukko on ääretön joukko – kokonaislukuja on ääretön määrä. Kokonaislukujen joukkoa merkitään symbolilla
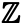
Parillisten lukujen joukko, jota voimme merkitä
määritellään
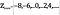
intuitiivisesti, voi näyttää siltä, että
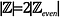
että jokaista parillista kokonaislukua kohti on 2 kokonaislukua: 1 pariton kokonaisluku ja 1 parillinen kokonaisluku. Todistetaan tämä.
Kokeillaan joukkojen vertailua kartoittamalla alkioita yhdestä joukosta toiseen.
Voidaan kartoittaa 1 2:een, 2 4:ään, 3 6:een ja niin edelleen.
Jos tämä jatkuu koko joukon läpi, näemme, että jokainen alkio kokonaislukujoukon joukosta karttuu täsmälleen yhteen alkioon parillisen kokonaislukujoukon joukosta.
Siten, vaikka se saattaa tuntua intuition vastaiselta, joukot ovat yhtä suuria.